Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-19T08:36:07.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact convergence rate of an Erdös-Rényi strong law for moving quantiles

Published online by Cambridge University Press:  14 July 2016

Paul Deheuvels  and
Josef Steinebach
Paul Deheuvels*
Affiliation:
Université de Paris
Josef Steinebach*
Affiliation:
Universität Marburg
*
∗Postal address: Institut de Statistique, Université de Paris VI, 4 Place Jussieu, F-75230 Paris Cedex 05, France.
∗∗Postal address: Fachbereich Mathematik, Philipps-Universität, Hans-Meerwein-Straße, D-3550 Marburg, W. Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a sequence U1, U2, · ·· of i.i.d. uniform (0, 1)-random variables. For fixed α ∈ (0, 1), let U(n, K) denote the [Kα]th order statistic of the subsample Un+1, · ··, Un+K, and set 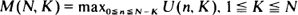. Book and Truax (1976) proved the following analogue of the Erdös-Rényi (1970) strong law of large numbers: for α < u < 1 and C = C(α, u) such that −1/C = αlog(u/α)+ (1 – α)log((l – u)/(1 –α)), it holds almost surely that 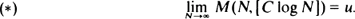In view of the Deheuvels–Devroye (1983) improvements of the original Erdös-Rényi law, we determine the lim inf and lim sup of 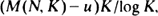where K = [C log N]. This improves (∗), showing that it holds with a best-possible convergence rate of order O(log log N/log N). Using the quantile transformation the result can be extended to a general i.i.d. sequence X1, X2, · ·· with d.f. F satisfying a strict monotonicity condition.

Keywords

BEST STRONG CONVERGENCE RATEMAXIMUM MOVING QUANTILESLARGE DEVIATIONSSTOCHASTIC GEYSER PROBLEM
Type
Research Paper
Information
Journal of Applied Probability , Volume 23 , Issue 2 , June 1986 , pp. 355 - 369
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bahadur, R. R. and Ranga Rao, R. (1960) On deviations of the sample mean. Ann. Math. Statist. 31, 1015–1027.Google Scholar
Bartfai, P. (1966) Die Bestimmung der zu einem wiederkehrenden Prozeß gehörenden Verteilungsfunktion aus den mit Fehlern behafteten Daten einer einzigen Realisation. Studia Sci. Math. Hung. 1, 161–168.Google Scholar
Book, S. A. (1979) The stochastic geyser problem for sample quantiles. J. Appl. Prob. 16, 445–448.Google Scholar
Book, S. A. and Truax, D. R. (1976) An Erdös-Rényi strong law for sample quantiles. J. Appl. Prob. 13, 578–583.Google Scholar
Chung, K. L. and Erdös, P. (1952) On the application of the Borel–Cantelli lemma. Trans. Amer. Math. Soc. 72, 179–186.Google Scholar
Csörgö, M. and Revesz, P. (1981) Strong Approximations in Probability and Statistics. Academic Press, New York.Google Scholar
Csörgö, M. and Steinebach, J. (1981) Improved Erdös-Rényi and strong approximation laws for increments of partial sums. Ann. Prob. 9, 988–996.Google Scholar
Csörgö, S. (1979) Erdös-Rényi laws. Ann. Statist. 7, 772–787.Google Scholar
Deheuvels, P. and Devroye, L. (1983) Limit laws related to the Erdös-Rényi theorem. Tech. Rep. No. 6, LSTA, Université Paris VI.Google Scholar
Deheuvels, P., Devroye, L. and Lynch, J. (1986) Exact convergence rates in the limit theorems of Erdös-Rényi and Shepp. Ann. Prob. Google Scholar
Erdös, P. and Renyi, A. (1970) On a new law of large numbers. J. Anal. Math. 23, 103–111.Google Scholar
Petrov, V. V. (1965) On the probabilities of large deviations of sums of independent random variables. Theory Prob. Appl. 10, 287–298.Google Scholar
Renyi, A. (1962) A sztochasztikus gejzir (Vortragsauszug). Publ. Math. Inst. Hung. Acad. Sci. 7, 643.Google Scholar
Sarkadi, K. and Vincze, I. (1974) Mathematical Methods of Statistical Quality Control. Academic Press, New York.Google Scholar
Steinebach, J. (1984) Between invariance principles and Erdös-Rényi laws. In Limit Theorems in Probability and Statistics, ed. Révész, P., North-Holland, Amsterdam, 981–1005.Google Scholar