Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T13:14:39.337Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimation of integrals with respect to infinite measures using regenerative sequences

Part of: Probabilistic methods, simulation and stochastic differential equations Limit theorems

Published online by Cambridge University Press:  30 March 2016

Krishna B. Athreya  and
Vivekananda Roy
Krishna B. Athreya*
Affiliation:
Iowa State University
Vivekananda Roy*
Affiliation:
Iowa State University
*
∗Postal address: Department of Mathematics, Iowa State University, Ames, IA 50011, USA.
∗∗Postal address: Department of Statistics, Iowa State University, Ames, IA 50011, USA. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f be an integrable function on an infinite measure space (S, 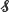, π). We show that if a regenerative sequence {Xn}n≥0 with canonical measure π could be generated then a consistent estimator of λ ≡ ∫Sf dπ can be produced. We further show that under appropriate second moment conditions, a confidence interval for λ can also be derived. This is illustrated with estimating countable sums and integrals with respect to absolutely continuous measures on ℝd using a simple symmetric random walk on ℤ.

Keywords

Markov chainMonte Carloimproper targetrandom walkregenerative sequence

MSC classification

Primary: 65C05: Monte Carlo methods
Secondary: 60F05: Central limit and other weak theorems
Type
Research Papers
Information
Journal of Applied Probability , Volume 52 , Issue 4 , December 2015 , pp. 1133 - 1145
Copyright
Copyright © Applied Probability Trust 2015 

References

[1] Asmussen, S. and Glynn, P. W. (2007). Stochastic Simulation: Algorithms and Analysis. Springer, New York.Google Scholar
[2] Athreya, K. B. and Roy, V. (2014). Monte Carlo methods for improper target distributions. Electron. J. Statist. 8, 2664–2692.Google Scholar
[3] Baron, M. and Rukhin, A. L. (1999). Distribution of the number of visits of a random walk. Commun. Statist. Stoch. Models 15, 593–597.Google Scholar
[4] Billingsley, P. (1968). Convergence of Probability Measures. John Wiley, New York.Google Scholar
[5] Casella, G. and George, E. I. (1992). Explaining the Gibbs sampler. Amer. Statistician 46, 167–174.Google Scholar
[6] Crane, M. A. and Iglehart, D. L. (1975). Simulating stable stochastic systems. III. Regenerative processes and discrete-event simulations. Operat. Res. 23, 33–45.Google Scholar
[7] Durrett, R. (2010). Probability: Theory and Examples , 4th edn. Cambridge University Press.CrossRefGoogle Scholar
[8] Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. II, 2nd edn. John Wiley, New York.Google Scholar
[9] Glynn, P. W. and Iglehart, D. L. (1987). A joint central limit theorem for the sample mean and regenerative variance estimator. Ann. Operat. Res. 8, 41–55.Google Scholar
[10] Hobert, J. P., Jones, G. L., Presnell, B. and Rosenthal, J. S. (2002). On the applicability of regenerative simulation in Markov chain Monte Carlo. Biometrika 89, 731–743.Google Scholar
[11] Karlsen, H. A. and Tj⊘Stheim, D. (2001). Nonparametric estimation in null recurrent time series. Ann. Statist. 29, 372–416.CrossRefGoogle Scholar
[12] Kasahara, Y. (1984). Limit theorems for Lévy processes and Poisson point processes and their applications to Brownian excursions. J. Math. Kyoto Univ. 24, 521–538.Google Scholar
[13] Metropolis, N. et al. (1953). Equations of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092.CrossRefGoogle Scholar
[14] Meyn, S. P. and Tweedie, R. L. (1993). Markov Chains and Stochastic Stability. Springer, London.CrossRefGoogle Scholar
[15] Mykland, P., Tierney, L. and Yu, B. (1995). Regeneration in Markov chain samplers. J. Amer. Statist. Assoc. 90, 233–241.Google Scholar
[16] Robert, C. P. and Casella, G. (2004). Monte Carlo Statistical Methods , 2nd edn. Springer, New York.Google Scholar
[17] R Development Core Team (2011). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing Vienna, Austria. Available at http://www.r-project.org.Google Scholar
[18] Skorokhod, A. V. (1957). Limit theorems for stochastic processes with independent increments. Theory Prob. Appl. 2, 138–171.Google Scholar