Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T04:55:32.353Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating the home range

Part of: Stochastic processes Probability theory on algebraic and topological structures Nonparametric inference Limit theorems

Published online by Cambridge University Press:  14 July 2016

L. De Haan  and
Sidney Resnick
L. De Haan*
Affiliation:
Erasmus University Rotterdam
Sidney Resnick*
Affiliation:
Cornell University
*
∗ Postal address: Econometric Institute, Erasmus University Rotterdam, P.O. Box 1738, 3000 DR Rotterdam, The Netherlands.
∗∗ Postal address: School of Operations Research and Industrial Engineering, Cornell University, Ithaca, NY 14853–7501, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

A proposal is given for estimating the home range of an animal based on sequential sightings. We assume the given sightings are independent, identically distributed random vectors X1,· ··, Xn whose common distribution has compact support. If 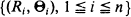are the polar coordinates of the sightings, then is a sup-measure and corresponds to the right endpoint of the distribution 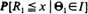. The corresponding upper semi-continuous function l(θ) is the boundary of the home range. We give a consistent estimator for the boundary l and under the assumption that the distribution of R1 given 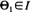is in the domain of attraction of an extreme value distribution with bounded support, we are able to give an approximate confidence region.

Keywords

UPPER SEMI-CONTINUOUS FUNCTIONSSUP-MEASURESEXTREME VALUE DISTRIBUTION

MSC classification

Primary: 60B10: Convergence of probability measures
Secondary: 60F05: Central limit and other weak theorems 60G70: Extreme value theory; extremal processes 62G05: Estimation 62G20: Asymptotic properties
Type
Research Papers
Information
Journal of Applied Probability , Volume 31 , Issue 3 , September 1994 , pp. 700 - 720
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was partially supported by the Forschungsinstitut für Mathematik, ΕTH, Zürich and by Nato Collaborative Research Grant CRG 901020. The hospitality of Professor Paul Embrechts and ETH Zürich, Cornell's School of Operations Research and Industrial Engineering and Erasmus University is gratefully acknowledged. S. Resnick was also partially supported by NSF Grant MCS 9100027 at Cornell University.

References

Bingham, N. H. (1992) On estimating a convex set. Preprint.Google Scholar
Castaing, C. and Valadier, M. (1977) Convex Analysis and Measurable Multifunctions. Lecture Notes in Mathematics 580, Springer-Verlag, New York.CrossRefGoogle Scholar
Dekkers, A., Einmahl, J. and Haan, L. De (1989) A moment estimator for the index of an extreme value distribution. Ann. Statist. 17, 1833–1855.Google Scholar
Dolecki, S., Salinetti, G. and Wets, R. (1983) Convergence of functions: equi-continuity. Trans. Amer. Math. Soc. 276, 409–429.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. 1, 3rd edn. Wiley, New York.Google Scholar
Macdonald, D. W., Ball, F. G. and Hough, N. G. (1980) The evaluation of home range size and configuration using radio tracking. In Handbook on Telemetry and Radio Tracking. Pergamon Press, Oxford.Google Scholar
Norberg, T. (1986) Random capacities and their distributions. Prob. Theory. Rel. Fields 73, 281–297.Google Scholar
Resnick, S. (1987) Extreme Values, Regular Variation and Point Processes. Springer-Verlag, New York.Google Scholar
Resnick, S. (1992) Adventures in Stochastic Processes. Birkhauser, Boston.Google Scholar
Vervaat, W. (1988) Random upper semicontinuous functions and extremal processes. In Probability and Lattices, CWI Tract, Amsterdam. To appear.Google Scholar