Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-09T01:30:38.492Z Has data issue: false hasContentIssue false
  • English
  • Français

Efficient conditional Monte Carlo simulations for the exponential integrals of Gaussian random fields

Part of: Stochastic processes Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  08 February 2022

Quang Huy Nguyen  and
Christian Y. Robert Open the ORCID record for Christian Y. Robert [Opens in a new window]
Quang Huy Nguyen*
Affiliation:
National Economics University
Christian Y. Robert*
Affiliation:
Center for Research in Economics and Statistics, ENSAE and Université de Lyon
*
*Postal address: Faculty of Mathematical Economics, National Economics University, Hanoi, Vietnam. Email: [email protected]
**Postal adress: Laboratory in Finance and Insurance - LFA CREST - Center for Research in Economics and Statistics, ENSAE, Paris, France. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a continuous Gaussian random field living on a compact set 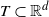$T\subset \mathbb{R}^{d}$ . We are interested in designing an asymptotically efficient estimator of the probability that the integral of the exponential of the Gaussian process over T exceeds a large threshold u. We propose an Asmussen–Kroese conditional Monte Carlo type estimator and discuss its asymptotic properties according to the assumptions on the first and second moments of the Gaussian random field. We also provide a simulation study to illustrate its effectiveness and compare its performance with the importance sampling type estimator of Liu and Xu (2014a).

Keywords

Exponential integralAsmussen–Kroese estimatorlogarithmically efficient estimatorsrare event simulation

MSC classification

Primary: 65C05: Monte Carlo methods
Secondary: 60G15: Gaussian processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 366 - 383
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S., Blanchet, J., Juneja, S. and Rojas-Nandayapa, L. (2011). Efficient simulation of tail probabilities of sums of correlated lognormals. Ann. Operat. Res. 189, 5–23.10.1007/s10479-009-0658-5CrossRefGoogle Scholar
Asmussen, S. and Glynn, P. (2007). Stochastic Simulation: Algorithms and Analysis. Springer, New York.10.1007/978-0-387-69033-9CrossRefGoogle Scholar
Kortschak, D., and Hashorva, E. (2013). Efficient simulation of tail probabilities for sums of log-elliptical risks. J. Comput. Appl. Math. 247, 53–67.10.1016/j.cam.2012.11.025CrossRefGoogle Scholar
Liu, J. (2012). Tail approximations of integrals of Gaussian random fields. Ann. Prob. 40, 1069–1104.10.1214/10-AOP639CrossRefGoogle Scholar
Liu, J. and Xu, G. (2014a). Efficient simulations for the exponential integrals of Hölder continuous Gaussian random fields. ACM Trans. Model. Comput. Simul. 24, 9.10.1145/2567892CrossRefGoogle Scholar
Liu, J. and Xu, G. (2014b). On the conditional distributions and the efficient simulations of exponential integrals of Gaussian random fields. Ann. Appl. Prob. 24, 1691–1738.10.1214/13-AAP960CrossRefGoogle Scholar