Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T20:55:36.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Drift vectors are not sufficient to determine recurrence of a Markov chain on ℤ3+

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

Mitchell Kotler
Mitchell Kotler*
Affiliation:
University of Massachusetts, Amherst
*
∗Postal address: Department of Mathematics and Statistics, UMass Amherst, Amherst, MA 01003, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

For a Markov chain in 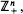n = 2, drift vectors (conditional expected jumps) on the interior and the boundaries distinguish between recurrence and transience. The result of this paper is that the analogous proposition in the n = 3 case fails.

Keywords

ERGODICLYAPOUNOV FUNCTIONTRANSIENT

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Journal of Applied Probability , Volume 31 , Issue 4 , December 1994 , pp. 1098 - 1102
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Fayolle, G. (1989) On random walks arising in queueing systems: ergodicity and transience via quadratic forms as Lyapounov functions – Part I. Queueing Systems 5, 167–184.CrossRefGoogle Scholar
Foster, F. G. (1953) On the stochastic matrices associated with certain queueing processes. Ann. Math. Statist. 24, 355–360.CrossRefGoogle Scholar
Malyshev, V. A. (1972) Classification of two-dimensional positive random walks and almost linear semi-martingales. Sov. Math. Dokl. 13, 136–139.Google Scholar
Rosenkrantz, W. (1989) Ergodicity conditions for two-dimensional Markov chains on the positive quadrant. Prob. Theory Rel. Fields 83, 309–319.Google Scholar