Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-12T19:42:02.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Detailed probabilistic analysis of the integrated three-valued telegraph signal

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

Ilaria Di Matteo  and
Enzo Orsingher
Ilaria Di Matteo*
Affiliation:
University of Rome ‘La Sapienza'
Enzo Orsingher*
Affiliation:
University of Rome ‘La Sapienza'
*
∗Postal address: Dipartimento di Statistica, Probabilità e Statistiche Applicate, University of Rome ‘La Sapienza', Piazzale Aldo Moro 5, 00185 Rome, Italy.
∗Postal address: Dipartimento di Statistica, Probabilità e Statistiche Applicate, University of Rome ‘La Sapienza', Piazzale Aldo Moro 5, 00185 Rome, Italy.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper the integrated three-valued telegraph process 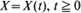is examined. In particular, the third-order equations governing the distributions 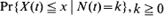, (where N(t) denotes the number of changes of the telegraph process up to time t) are derived and recurrence relationships for them are obtained by solving suitable initial-value problems. These recurrence formulas are related to the Fourier transform of the conditional distributions and are used to obtain explicit results for small values of k. The conditional mean values 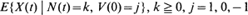(where V(0) denotes the initial velocity of motions) are obtained and discussed.

Keywords

HYPERBOLIC EQUATIONSPOISSON PROCESSINITIAL-VALUE PROBLEMSFOURIER TRANSFORMSFORCED WAVE EQUATION

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 3 , September 1997 , pp. 671 - 684
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, A. and Renshaw, E. (1994) The general correlated random walk. J. Appl. Prob. 31, 869–884.Google Scholar
Foong, S. K. and Kanno, S. (1994) Properties of the telegrapher's random process with or without a trap. Stoch. Proc. Appl. 53, 147–173.CrossRefGoogle Scholar
Jakeman, E. and Renshaw, E. (1987) Correlated random-walk model for scattering. J. Opt. Soc. Amer. A 4, 1206–1212.Google Scholar
Kolesnik, A. D. (1990) One dimensional models of the Markovian random evolutions. Preprint 90.57. Kiev Inst. Math. (In Russian.) Google Scholar
Orsingher, E. (1990a) Probability law, flow functions, maximum distributions of wave-governed random motions and their connections with Kirchhoff's laws. Stoch. Proc. Appl. 34, 49–62.Google Scholar
Orsingher, E. (1990b) Random motions governed by third-order equations. Adv. Appl. Prob. 22, 915–928.Google Scholar
Orsingher, E. and Bassan, B. (1992) On a 2n-valued telegraph signal and the related integrated process. Stoch. Stoch. Rep. 38, 159–173.Google Scholar
Renshaw, E. and Henderson, R. (1981) The correlated random walk. J. Appl. Prob. 18, 403–414.CrossRefGoogle Scholar