Article contents
Denumerable Markov processes with bounded generators: a routine for calculating pij(∞)
Published online by Cambridge University Press: 14 July 2016
Extract
1. Let the (honest) Markov process with transition functions (pij(0)) have transition rates (qij) and suppose that, for some M,
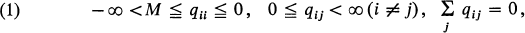 so that the matrix Q = (qij) determines a bounded operator on the Banach space l1 by right-multiplication. Then in the terminology of [8], (pp. 12 and 19) Q will be bounded and ΩF will be a closed restriction of Q with dense domain, so that ΩF = Q; that is, we shall have a process whose associated semigroup has a bounded generator. In these circumstances Theorem 10.3.2 of [2] applies and the matrix Pt = (pij(t)) is given by
so that the matrix Q = (qij) determines a bounded operator on the Banach space l1 by right-multiplication. Then in the terminology of [8], (pp. 12 and 19) Q will be bounded and ΩF will be a closed restriction of Q with dense domain, so that ΩF = Q; that is, we shall have a process whose associated semigroup has a bounded generator. In these circumstances Theorem 10.3.2 of [2] applies and the matrix Pt = (pij(t)) is given by
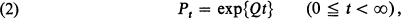 where exp{·} denotes the function defined by the exponential power-series. We shall be interested here (as in [5] and [9]) in the determination of the limit matrix P∞ = (limt→∞pij(t)).
where exp{·} denotes the function defined by the exponential power-series. We shall be interested here (as in [5] and [9]) in the determination of the limit matrix P∞ = (limt→∞pij(t)).
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1971
References
- 5
- Cited by


