Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T20:59:28.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical scaling for the SIS stochastic epidemic

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

R. G. Dolgoarshinnykh  and
Steven P. Lalley
R. G. Dolgoarshinnykh*
Affiliation:
Columbia University
Steven P. Lalley*
Affiliation:
University of Chicago
*
∗Postal address: Department of Statistics, Columbia University, New York, NY 10027, USA. Email address: [email protected]
∗∗Postal address: Department of Statistics, University of Chicago, Chicago, IL 60637, USA. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

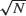We exhibit a scaling law for the critical SIS stochastic epidemic. If at time 0 the population consists of infected and 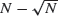susceptible individuals, then when the time and the number currently infected are both scaled by 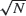, the resulting process converges, as N → ∞, to a diffusion process related to the Feller diffusion by a change of drift. As a consequence, the rescaled size of the epidemic has a limit law that coincides with that of a first passage time for the standard Ornstein-Uhlenbeck process. These results are the analogs for the SIS epidemic of results of Martin-Löf (1998) and Aldous (1997) for the simple SIR epidemic.

Keywords

Stochastic epidemic modelSISSIRFeller diffusionOrnstein-Uhlenbeck process

MSC classification

Primary: 60K30: Applications (congestion, allocation, storage, traffic, etc.)
Secondary: 92D30: Epidemiology
Type
Research Article
Information
Journal of Applied Probability , Volume 43 , Issue 3 , September 2006 , pp. 892 - 898
Copyright
© Applied Probability Trust 2006 

References

Aldous, D. (1997). Brownian excursions, critical random graphs and the multiplicative coalescent. Ann. Prob. 25, 812–854.CrossRefGoogle Scholar
Darling, D. A. and Siegert, A. J. F. (1953). The first passage problem for a continuous Markov process. Ann. Math. Statist. 24, 624–639.Google Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes. Characterization and Convergence. John Wiley, New York.CrossRefGoogle Scholar
Feller, W. (1951). Diffusion processes in genetics. In Proc. 2nd Berkeley Symp. Math. Statist. Prob., 1950, University of California Press, Berkeley and Los Angeles, pp. 227–246.Google Scholar
Friedman, A. (1964). Partial Differential Equations of Parabolic Type. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
Jiřina, M. (1969). On Feller's branching diffusion processes. Časopis Pěst. Mat. 94, 84–90, 107.Google Scholar
Kryscio, R. J. and Lefèvre, C. (1989). On the extinction of the S-I-S stochastic logistic epidemic. J. Appl. Prob. 26, 685–694.Google Scholar
Lindvall, T. (1974). On Feller's branching diffusion processes. Adv. Appl. Prob. 6, 309–321.Google Scholar
Martin-Löf, A. (1998). The final size of a nearly critical epidemic, and the first passage time of a Wiener process to a parabolic barrier. J. Appl. Prob. 35, 671–682.CrossRefGoogle Scholar
Nasell, I. (1996). The quasi-stationary distribution of the closed endemic SIS model. Adv. Appl. Prob. 28, 895–932.CrossRefGoogle Scholar
Nasell, I. (1999). On the time to extinction in recurrent epidemics. J. R. Statist. Soc. B 61, 309–330.Google Scholar
Norden, R. H. (1982). On the distribution of the time to extinction in the stochastic logistic population model. Adv. Appl. Prob. 14, 687–708.Google Scholar
Weiss, G. and Dishon, M. (1971). On the asymptotic behavior of the stochastic and deterministic models of an epidemic. Math. Biosci. 11, 261–265.Google Scholar