Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T09:02:02.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical behavior of percolation and Markov fields on branching planes

Part of: Equilibrium statistical mechanics Special processes

Published online by Cambridge University Press:  14 July 2016

C. Chris Wu
C. Chris Wu*
Affiliation:
Courant Institute of Mathematical Sciences, New York
*
∗ Present address: Department of Mathematics, Penn State University, Beaver Campus, Monaca, PA 15061, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

For an independent percolation model on 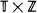, where 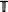is a homogeneous tree and 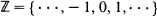is a one-dimensional lattice, it is shown, by verifying that the triangle condition is satisfied, that the percolation probability θ (p) is a continuous function of p at the critical point pc, and the critical exponents 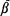, γ, δ, and Δ exist and take their mean-field values. Some analogous results for Markov fields on 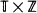are also obtained.

Keywords

GIBBS MEASURECRITICAL EXPONENTSPOWER LAWSMEAN-FIELD VALUESISING MODELSMAGNETIZATION

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82B27: Critical phenomena
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 3 , September 1993 , pp. 538 - 547
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by NSF Grants DMS-8902156 and DMS-9196086.

References

Aizenman, M. (1985) Rigorous studies of critical behavior, II. In Statistical Physics and Dynamical Systems: Rigorous Results, ed. Fritz, J., Jaffe, A., and Szász, D. Birkhäuser, Boston.Google Scholar
Aizenman, M. and Barsky, D. J. (1987) Sharpness of the phase transition in percolation models. Commun. Math. Phys. 108, 489–526.Google Scholar
Aizenman, M. and Fernández, R. (1986) On the critical behavior of the magnetization in high-dimensional Ising models. J. Statist. Phys. 44, 393–454.Google Scholar
Aizenman, M. and Newman, C. M. (1984) Tree graph inequalities and critical behavior in percolation models. J. Statist. Phys. 36, 107–143.Google Scholar
Aizenman, M., Chayes, J. T., Chayes, L. and Newman, C. M. (1988) Discontinuity of the magnetization in one-dimensional 1/(|x - y |2) Ising and Potts models. J. Statist. Phys. 50, 1–40.Google Scholar
Barsky, D. J. and Aizenman, M. (1991) Percolation critical exponents under the triangle condition. Ann. Prob. 19, 1520–1536.Google Scholar
Van Den Berg, J. and Keane, M. (1984) On the continuity of the percolation probability function. Contemp. Math. 26, 61–65.Google Scholar
Durrett, R. (1988) Lecture Notes on Particle Systems and Percolation. Wadsworth and Brooks/Cole, Monterey, California.Google Scholar
Grimmett, G. R. (1989) Percolation. Springer-Verlag, Berlin.Google Scholar
Grimmett, G. R. and Newman, C. M. (1989) Percolation in 8 + 1 dimensions. In Disorder in Physical Systems, ed. Grimmett, G. R. and Welsh, D. J. A., pp. 167–190. Oxford University Press.Google Scholar
Hara, T. and Slade, G. (1990) Mean-field critical phenomena for percolation in high dimensions. Commun. Math. Phys. 128, 333–391.Google Scholar
Harris, T. E. (1960) A lower bound for the critical probability in a certain percolation process. Proc. Camb. Phil. Soc. 56, 13–20.Google Scholar
Kesten, H. (1980) The critical probability of bond percolation on the square lattice equals. Commun. Math. Phys. 74, 41–59.Google Scholar
Kesten, H. (1982) Percolation Theory for Mathematicians. Birkhäuser, Boston.Google Scholar
Menshikov, M. V. (1986) Coincidence of critical points in percolation problems. Soviet Math. Dokl. 33, 856–859.Google Scholar
Newman, C. M. (1987) Shock waves and mean field bounds. Concavity and analyticity of the magnetization at low temperature. Appendix to Percolation theory: A selective survey of rigorous results. In Advances in Multiphase Flow and Related Problems. ed. Papanicolaou, G. SIAM, Philadelphia.Google Scholar
Newman, C. M. and Wu, C. (1990) Markov fields on branching planes. Prob. Theory Rel. Fields 85, 539–552.Google Scholar
Nguyen, B. G. (1987) Gap exponents for percolation processes. J. Statist. Phys. 49, 235–243.Google Scholar
Pemantle, R. (1990) The contact process on trees: a beginning. Preprint.Google Scholar