Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-18T16:23:09.489Z Has data issue: false hasContentIssue false
  • English
  • Français

The control of a finite dam with penalty cost function: Markov input rate

Published online by Cambridge University Press:  14 July 2016

F. A. Attia
F. A. Attia*
Affiliation:
Kuwait University
*
∗Postal address: Department of Mathematics, Kuwait University, P.O. Box 5969, Kuwait.
Get access Rights & Permissions [Opens in a new window]

Abstract

The long-run average cost per unit time of operating a finite dam controlled by a 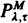policy (Lam Yeh (1985)) is determined when the cumulative input process is the integral of a Markov chain. A penalty cost which accrues continuously at a rate g(X(t)), where g is a bounded measurable function of the content, is also introduced. An example where the input rate is a two-state Markov chain is considered in detail to illustrate the computations.

Keywords

STOPPING TIMEGENERATORINTEGRAL OF MARKOV CHAIN
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 2 , June 1987 , pp. 457 - 465
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by Kuwait University Research Grant No. SM 030.

References

Attia, F. A. and Brockwell, P. J. (1982) The control of a finite dam. J. Appl. Prob. 19, 815–825.Google Scholar
Faddy, ?. J. (1974) Optimal control of finite dams: discrete (2-stage) output procedure. J. Appl. Prob. 11, 111–121.Google Scholar
Karlin, S. and Taylor, H. M. (1981) A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
Yeh, Lam (1983) Optimal control of a finite dam: average-cost case. J. Appl. Prob. 22, 480–484.Google Scholar
Zuckerman, D. (1977) Two-stage output procedure of a finite dam. J. Appl. Prob. 14, 421–425.Google Scholar