Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T06:55:11.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity and convergence of the percolation function in continuum percolation

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

Anish Sarkar
Anish Sarkar*
Affiliation:
University of Utrecht
*
∗Postal address: Department of Mathematics, University of Utrecht, PO Box 80.010, 3508 TA Utrecht, The Netherlands.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a percolation model on the d-dimensional Euclidean space 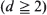which consists of spheres centred at the points of a Poisson point process of intensity ?. The radii of the spheres are random and are chosen independently and identically according to a distribution of a positive random variable. We show that the percolation function is continuous everywhere except perhaps at the critical point. Further, we show that the percolation functions converge to the appropriate percolation function except at the critical point when the radius random variables are uniformly bounded and converge weakly to another bounded random variable.

Keywords

POISSON PROCESSPERCOLATION FUNCTIONSCALINGCOUPLING

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60K10: Applications (reliability, demand theory, etc.)
Type
Research Article
Information
Journal of Applied Probability , Volume 34 , Issue 2 , June 1997 , pp. 363 - 371
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alexander, K. (1993) Finite clusters in high-density continuous percolation: compression and sphericality. Prob. Theory Rel. Fields 97, 35–63.Google Scholar
[2] Van Den Berg, J. and Keane, M. (1984) On the continuity of the percolation probability function. In Conference on Modern Analysis and Probability. ed. Beals, R. et al. AMS, Providence, RI. pp. 61–65.Google Scholar
[3] Grimmett, G. (1988) Percolation. Springer, New York.Google Scholar
[4] Hall, P. (1985) On continuum percolation. Ann. Prob. 13, 1250–1266.CrossRefGoogle Scholar
[5] Hall, P. (1988) Introduction to the Theory of Coverage Processes. Wiley. New York.Google Scholar
[6] Meester, R. and Roy, R. (1994) Uniqueness of the unbounded occupied and vacant components in Boolean models. Ann. Appl. Prob. 4, 933–951.Google Scholar
[7] Meester, R. and Roy, R. (1996) Continuum Percolation. Cambridge University Press, New York.Google Scholar
[8] Meester, R., Roy, R. and Sarkar, A. (1994) Non-universality and continuity of the critical covered volume fraction in continuum percolation. J. Statist. Phys. 75, 123–134.Google Scholar
[9] Menshikov, M. V., Molchanov, S. A. and Sidorenko, A. F. (1986) Percolation theory and some applications. J. Soviet Math. 42, 1766–1810.CrossRefGoogle Scholar
[10] Penrose, M. D. (1994) Euclidean minimal spanning trees and continuum percolation in high dimensions. Preprint. Google Scholar
[11] Roy, R. (1990) The RSW theorem and the equality of critical densities and the ‘dual’ critical densities for continuum percolation on 2. Ann. Prob. 18, 1563–1575.Google Scholar