Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Iosifescu, Marius
1983.
Mathematical Learning Models — Theory and Algorithms.
Vol. 20,
Issue. ,
p.
86.
Stadje, Wolfgang
1997.
Asymptotic normality of discounted random series with applications in reliability and queueing.
Operations Research Letters,
Vol. 20,
Issue. 5,
p.
229.


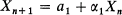 with probability π
with probability π with probability π
with probability π