Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T21:15:38.097Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of convergence rates for the approximation of the stationary distribution of infinite monotone stochastic matrices

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

F. Simonot  and
Y. Q. Song
F. Simonot*
Affiliation:
Université Henri Poincaré
Y. Q. Song*
Affiliation:
CRIN-ENSEM
*
∗Postal address: ESSTIN-Université Henri Poincaré, Nancy 1, Parc R Bentz, 54 500 Vandoeuvre, France. email:[email protected]
∗∗Postal address: CRIN-ENSEM, 2, av. de la Forêt de Haye, 54 516 Vandoeuvre, France. email:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let P be an infinite irreducible stochastic matrix, recurrent positive and stochastically monotone and Pn be any n × n stochastic matrix with Pn ≧ Tn, where Tn denotes the n × n northwest corner truncation of P. These assumptions imply the existence of limit distributions π and πn for P and Pn respectively. We show that if the Markov chain with transition probability matrix P meets the further condition of geometric recurrence then the exact convergence rate of πn to π can be expressed in terms of the radius of convergence of the generating function of π. As an application of the preceding result, we deal with the random walk on a half line and prove that the assumption of geometric recurrence can be relaxed. We also show that if the i.i.d. input sequence (A(m)) is such that we can find a real number r0 > 1 with 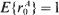, then the exact convergence rate of πn to π is characterized by r0. Moreover, when the generating function of A is not defined for |z| > 1, we derive an upper bound for the distance between πn and π based on the moments of A.

Keywords

MARKOV CHAINSTOCHASTIC MONOTONICITYRIGHT-BANDED MATRIXGEOMETRIC RECURRENCECONVERGENCE RATERANDOM WALKLINDLEY PROCESS

MSC classification

Secondary: 60K99: None of the above, but in this section
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 4 , December 1996 , pp. 974 - 985
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. (1987) Applied Probability and Queues. Wiley, New York.Google Scholar
Bhat, N. (1984) Elements of Applied Stochastic Processes. 2nd edn. Wiley, New York.Google Scholar
Borovkov, A. A. (1976) Stochastic Processes in Queueing Theory. Springer, New York.CrossRefGoogle Scholar
Chow, Y. S. and Teicher, H. (1988) Probability Theory. 2nd edn. Springer, New York.Google Scholar
Daley, D. J. (1968) Stochastically monotone Markov chains, Z. Wahrscheinlichkeitsth. 10, 305–317 Google Scholar
Gibson, D. and Seneta, E. (1987) Monotone infinite stochastic matrices and their augmented truncations. Stoch. Proc. Appl. 24, 287–292.CrossRefGoogle Scholar
Heyman, D. P. (1991) Approximating the stationary distribution of an infinite stochastic matrix. J. Appl. Prob. 28, 96–103.Google Scholar
Heyman, D. P. and Whitt, W. (1989) Limits of queues as the waiting room grows. QUESTA 5, 381–392.Google Scholar
Kalashnikov, V. V. (1994) Mathematical Methods in Queueing Theory , Kluwer, Dordrecht.Google Scholar
Kalashnikov, V. V. and Rachev, S. T. (1990) Mathematical Methods for Construction of Queueing Models. Wadsworth and Brooks Cole, London.Google Scholar
Karr, A. F. (1975) Weak convergence of a sequence of Markov chains. Z. Wahrscheinlichkeitsth. 33, 41–48.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993) Markov Chains and Stochastic Stability. Springer, Berlin.Google Scholar
Nummelin, E. (1984) General Irreducible Markov Chains and Non-Negative Operators. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Seneta, E. (1980) Computing the stationary distribution for infinite Markov chains. Linear Algebra Appl. 34, 259–267.CrossRefGoogle Scholar
Seneta, E. (1981) Non-negative Matrices and Markov Chains. 2nd edn. Springer, New York.Google Scholar
Simonot, F. (1995) Sur l'approximation de la distribution stationnaire d'une chaîne de Markov stochastiquement monotone. Stoch. Proc. Appl. 56, 133–149.Google Scholar
Stoyan, D. (1983) Comparison Methods for Queues and Other Stochastic Models. Wiley, New York.Google Scholar
Tijms, H. C. (1986) Stochastic Modelling and Analysis. Wiley, New York.Google Scholar
Tweedie, R. L. (1983) The existence of moments for stationary Markov chains. J. Appl. Prob. 20, 191–196.Google Scholar
Wolf, D. (1980) Approximation of the invariant probability distribution of an infinite stochastic matrix. Adv. Appl. Prob. 12, 710–726.Google Scholar