Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T05:13:43.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization by orthogonal polynomial systems of finite Markov chains

Part of: History of mathematics and mathematicians Markov processes

Published online by Cambridge University Press:  14 July 2016

E. Seneta
E. Seneta*
Affiliation:
University of Sydney
*
1Postal address: School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper characterizes matrices 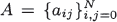which have a given system of vectors orthogonal with respect to a given probability distribution as its right eigenvectors. Results of Hoare and Rahman are unified in this context, then all matrices with a given orthogonal polynomial system as right eigenvectors under the constraint a0j = 0 for j ≥ 2 are specified. The only stochastic matrices P = {pij} satisfying p00 + p01 = 1 with the Hahn polynomials as right eigenvectors have the form of the Moran mutation model.

Keywords

Orthogonal polynomialsreversibilityMarkov chainsspectrumeigenvectorsChebyshevHahnKrawtchoukRacahMoran mutation modelhypergeometricself-dualityBernoulli-LaplaceEhrenfestVere-Jonesbirth-and-death processes

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 01A60: 20th century
Type
Markov chains
Information
Journal of Applied Probability , Volume 38 , Issue A: Probability, Statistics and Seismology , 2001 , pp. 42 - 52
Copyright
Copyright © Applied Probability Trust 2001 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, G. E., Askey, R. and Roy, R. (1999). Special Functions. Cambridge University Press.Google Scholar
Askey, R. and Wilson, J. (1979). A set of polynomials that generalize the Racah coefficients on 6 - j symbols. SIAM J. Math. Anal. 10, 1008–1016.Google Scholar
Chebyshev, P. L. (1875). Sur l'interpolation des valeurs équidistants. In Œuvres de P. L. Tchebychef , Tome II, eds Markoff, A. and Sonin, N., Chelsea, New York, 219–242. (1962 reprint. Volumes I and II originally published in St. Petersburg, 1899-1907).Google Scholar
Donnelly, P., Lloyd, P. and Sudbury, A. (1994). Approach to stationarity of the Bernoulli-Laplace diffusion model. Adv. Appl. Probab. 26, 715–727.Google Scholar
Dunkl, C. F. and Ramirez, D. E. (1974). Krawtchouk polynomials and the symmetrization of hypergroups. SIAM J. Math. Anal. 5, 351–366.CrossRefGoogle Scholar
Eagleson, G. K. (1969). A characterization theorem for positive definite sequences on the Krawtchouk polynomials. Austral. J. Statist , ll, 29–38.CrossRefGoogle Scholar
Hahn, W. (1949). Uber Orthogonalpolynome, die q-differenzengleichungen genügen. Math. Nachr. 2, 4–34.CrossRefGoogle Scholar
Heathcote, C. R., Seneta, E. and Vere-Jones, D. (1967). A refinement of two theorems in the theory of branching processes. Teor. Veroyatnost. i Primenen. 12, 297–301.Google Scholar
Hoare, M. R. and Rahman, M. (1983). Cumulative Bernoulli trials and Krawtchouk processes. Stoch. Proc. Applic. 16, 113–139.CrossRefGoogle Scholar
Karlin, S. and Mcgregor, J. L. (1961). The Hahn polynomials, formulas and an application. Scripta Math. 26, 33–46.Google Scholar
Karlin, S. and Mcgregor, J. L. (1962). On a genetics model of Moran. Proc. Cambridge Philos. Soc. 58, 299–231.CrossRefGoogle Scholar
Karlin, S. and Mcgregor, J. L. (1965). Ehrenfest urn models. J. Appl. Probab. 2, 352–376.CrossRefGoogle Scholar
Kemeny, J. G. and Snell, L. J. (1960). Finite Markov Chains. Van Nostrand, Princeton, NJ.Google Scholar
Kendall, M. G. and Stuart, A. (1963). The Advanced Theory of Statistics, Vol. 1, Distribution Theory. Griffin, London.Google Scholar
Moran, P. A. P. (1960). The Statistical Processes of Evolutionary Theory. Oxford University Press.Google Scholar
Seneta, E. (1997). M. Krawtchouk (1892-1942), Professor of Mathematical Statistics. Theory Stoch. Proc. 3, 388–392.Google Scholar
Seneta, E. (1998). Characterization of Markov chains by orthogonal polynomial systems. In Conference Materials, 7th Internat. Sci. Kravchuk Conf., 14-16 May 1998, Kyiv , Vipol, Kyiv, 454–457.Google Scholar
Seneta, E. and Vere-Jones, D. (1966). On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Probab. 3, 403–434.Google Scholar
Sneddon, I. N. (1961). Special Functions of Mathematical Physics and Chemistry. Oliver and Boyd, Edinburgh.Google Scholar
Vere-Jones, D. (1962). Geometric ergodicity in denumerable Markov chains. Quart. J. Math. Oxford (2) 13, 7–28.Google Scholar
Vere-Jones, D. (1967a). Ergodic properties of non-negative matrices, I. Pacific J. Math. 22, 361–386.Google Scholar
Vere-Jones, D. (1967b). The infinite divisibility of a bivariate gamma distribution. Sankhya A 29, 421–422.Google Scholar
Vere-Jones, D. (1968). Ergodic properties of non-negative matrices, II. Pacific J. Math. , 26, 601–620.Google Scholar
Vere-Jones, D. (1971). Finite bivariate distributions and semigroups of non-negative matrices. Quart. J. Math. Oxford (2) , 22, 247–270.Google Scholar