Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shi, Zhan
1998.
A local time curiosity in random environment.
Stochastic Processes and their Applications,
Vol. 76,
Issue. 2,
p.
231.
Comets, Francis
Gantert, Nina
and
Zeitouni, Ofer
2000.
Quenched, annealed and functional large deviations for one-dimensional random walk in random environment.
Probability Theory and Related Fields,
Vol. 118,
Issue. 1,
p.
65.
Bremont, Julien
2001.
On the recurrence of random walks on in random medium.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 333,
Issue. 11,
p.
1011.
Komorowski, T.
and
Krupa, G.
2001.
Random walk in a random environment with correlated sites.
Journal of Applied Probability,
Vol. 38,
Issue. 4,
p.
1018.
Brémont, Julien
2002.
On some random walks on Z in random medium.
The Annals of Probability,
Vol. 30,
Issue. 3,
Rassoul-Agha, Firas
2003.
The point of view of the particle on the law of large numbers for random walks in a mixing random environment.
The Annals of Probability,
Vol. 31,
Issue. 3,
Rassoul-Agha, Firas
2005.
On the Zero-One Law and the Law of Large Numbers for Random Walk in Mixing Random Environment.
Electronic Communications in Probability,
Vol. 10,
Issue. none,
Roitershtein, Alexander
2005.
A Log-scale Limit Theorem for One-dimensional Random Walks in Random Environments.
Electronic Communications in Probability,
Vol. 10,
Issue. none,
Zeitouni, Ofer
2006.
Random walks in random environments.
Journal of Physics A: Mathematical and General,
Vol. 39,
Issue. 40,
p.
R433.
Sznitman, Alain-Sol
2006.
Mathematical statistical physics, École d'ÉtÉ de physique des houches session LXXXIII.
Vol. 83,
Issue. ,
p.
219.
Roitershtein, Alexander
2007.
A note on multitype branching processes with immigration in a random environment.
The Annals of Probability,
Vol. 35,
Issue. 4,
Goldsheid, Ilya Ya.
2007.
Simple transient random walks in one-dimensional random environment: the central limit theorem.
Probability Theory and Related Fields,
Vol. 139,
Issue. 1-2,
p.
41.
Roitershtein, Alexander
2008.
Transient random walks on a strip in a random environment.
The Annals of Probability,
Vol. 36,
Issue. 6,
Goldsheid, Ilya Ya.
2008.
Linear and sub-linear growth and the CLT for hitting times of a random walk in random environment on a strip.
Probability Theory and Related Fields,
Vol. 141,
Issue. 3-4,
p.
471.
BRÉMONT, JULIEN
2009.
RANDOM WALK IN QUASI-PERIODIC RANDOM ENVIRONMENT.
Stochastics and Dynamics,
Vol. 09,
Issue. 01,
p.
47.
Brémont, Julien
2009.
One-dimensional finite range random walk in random medium and invariant measure equation.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 45,
Issue. 1,
Zeitouni, Ofer
2009.
Encyclopedia of Complexity and Systems Science.
p.
7520.
Yilmaz, Atilla
2009.
Quenched large deviations for random walk in a random environment.
Communications on Pure and Applied Mathematics,
Vol. 62,
Issue. 8,
p.
1033.
HONG, WENMING
and
ZHANG, LIN
2010.
BRANCHING STRUCTURE FOR THE TRANSIENT (1, R)-RANDOM WALK IN RANDOM ENVIRONMENT AND ITS APPLICATIONS.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 13,
Issue. 04,
p.
589.
Simula, Tapio
and
Stenlund, Mikko
2010.
Multi-Gaussian modes of diffusion in a quenched random medium.
Physical Review E,
Vol. 82,
Issue. 4,
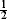 are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (Xn)’. In the case of uniquely ergodic (therefore non-independent) environments, this measure exists as soon as (Xn) is transient so that the ‘slow diffusion phenomenon’ does not appear as it does in the independent case. Thus, under regularity conditions, we prove that, in this case, the random walk satisfies a central limit theorem for any fixed environment.
are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (Xn)’. In the case of uniquely ergodic (therefore non-independent) environments, this measure exists as soon as (Xn) is transient so that the ‘slow diffusion phenomenon’ does not appear as it does in the independent case. Thus, under regularity conditions, we prove that, in this case, the random walk satisfies a central limit theorem for any fixed environment.

