Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T01:35:05.461Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of Markov renewal shock models

Part of: Special processes Operations research and management science

Published online by Cambridge University Press:  14 July 2016

Nobuko Igaki ,
Ushio Sumita  and
Masashi Kowada
Nobuko Igaki*
Affiliation:
Tezukayama University
Ushio Sumita*
Affiliation:
University of Rochester and International University of Japan
Masashi Kowada*
Affiliation:
Nagoya Institute of Technology
*
∗Postal address: Department of Management Information Systems and Decision Sciences, Tezukayama University 7−1−1 Tezukayama, Nara 631, Japan.
∗∗Postal address: William E. Simon Graduate School of Business Administration, University of Rochester, Rochester, NY 14627, USA, and Graduate School of International Management, International University of Japan, Yamato, Minami Uonuma, Niigata 942–72, Japan.
∗∗∗Postal address: Department of Mathematics for System Science, Nagoya Institute of Technology, Gokiso, Showa, Nagoya 466, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

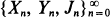A trivariate stochastic process is considered, describing a sequence of random shocks {Xn} at random intervals {Yn} with random system state {Jn}. The triviariate stochastic process satisfies a Markov renewal property in that the magnitude of shocks and the shock intervals are correlated pairwise and the corresponding joint distributions are affected by transitions of the system state which occur after each shock according to a Markov chain. Of interest is a system lifetime terminated whenever a shock magnitude exceeds a prespecified level z. The distribution of system lifetime, its moments and a related exponential limit theorem are derived explicitly. A similar transform analysis is conducted for a second type of system lifetime with system failures caused by the cumulative magnitude of shocks exceeding a fixed level z.

Keywords

SHOCK MODELMARKOV RENEWAL PROCESSRANDOM SYSTEM STATE

MSC classification

Primary: 60K20: Applications of Markov renewal processes (reliability, queueing networks, etc.)
Secondary: 90B25: Reliability, availability, maintenance, inspection
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 3 , September 1995 , pp. 821 - 831
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper has been partially supported by the NTT Research Fund.

References

[1] Esary, J. D., Marshall, A. W. and Proschan, F. (1973) Shock model and wear processes. Ann. Prob. 1, 627–649.Google Scholar
[2] Feng, W. (1992) Optimal Replacements Under Additive Damage in Random Environments, Ph.D. Dissertation, Nagoya Institute of Technology.Google Scholar
[3] Keilson, J. (1966) A limit theorem for passage times ergodic regenerative process. Ann. Math. Statist. 37, 866–870.Google Scholar
[4] Keilson, J. (1969) On the matrix renewal function for Markov renewal procecsses. Ann. Math. Statist. 40, 1901–1907.Google Scholar
[5] Keilson, J. (1979) Markov Chain Models — Rarity and Exponentiality. Springer-Verlag, New York.Google Scholar
[6] Shanthikumar, J. G. and Sumita, U. (1983) General shock models associated with correlated renewal sequences. J. Appl. Prob. 20, 600–614.Google Scholar
[7] Sumita, U. and Shanthikumar, J. G. (1985) A class of correlated cumulative shock models. Adv. Appl. Prob. 17, 347–366.Google Scholar
[8] Waldmann, K. H. (1983) Optimal replacement under additive damage in randomly varying environments. Naval Res. Logist. Quart. 30, 377–386.Google Scholar