Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T21:52:30.608Z Has data issue: false hasContentIssue false
  • English
  • Français

An optimal stopping problem for random walks with non-zero drift

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Markus Roters
Markus Roters*
Affiliation:
Universität Trier
*
∗Postal address: Universität Trier, FB IV Mathematik/Statistik, D-54286 Trier, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we give a solution of an optimal stopping problem concerning random walks 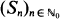with non-zero drift, thereby proving the necessity of the existence of ESτ for Wald's equation ESτ = ES1 · Ετ to hold, even if attention is restricted to non-randomized stopping times τ. This answers a question of Robbins and Samuel (1966).

Keywords

RANDOMIZED STOPPING TIMEWALD'S EQUATION

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 60G50: Sums of independent random variables; random walks
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 4 , December 1995 , pp. 956 - 959
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackwell, D. (1946) On an equation of Wald. Ann. Math. Statist. 17, 84–87.CrossRefGoogle Scholar
Kiefer, J. and Wolfowitz, J. (1956) On the characteristics of the general queueing process, with applications to random walk. Ann. Math. Statist. 27, 147–161.CrossRefGoogle Scholar
Ramakrishnan, S. and Sudderth, W. D. (1986) The expected value of an everywhere stopped martingale. Ann. Prob. 14, 1075–1079.CrossRefGoogle Scholar
Robbins, H. and Samuel, E. (1966) An extension of a lemma of Wald. J. Appl. Prob. 3, 272–273.CrossRefGoogle Scholar
Roters, M. (1994) On the validity of Wald's equation. J. Appl. Prob. 31, 949–957.CrossRefGoogle Scholar
Samuel, E. (1967) On the existence of the expectation of randomly stopped sums. J. Appl. Prob. 4, 197–200.CrossRefGoogle Scholar
Wald, A. (1945) Sequential tests of statistical hypotheses. Ann. Math. Statist. 16, 117–186.CrossRefGoogle Scholar