Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T05:30:13.740Z Has data issue: false hasContentIssue false
  • English
  • Français

An explicit Dobrushin uniqueness region for Gibbs point processes with repulsive interactions

Part of: Special processes

Published online by Cambridge University Press:  30 March 2022

Pierre Houdebert  and
Alexander Zass Open the ORCID record for Alexander Zass [Opens in a new window]
Pierre Houdebert*
Affiliation:
Universität Potsdam
Alexander Zass*
Affiliation:
Universität Potsdam, WIAS Berlin
*
*Postal address: Karl-Liebknecht Str. 24-25, 14476 Potsdam, Germany. Email: [email protected]
**Postal address: Mohrenstr. 39, 10117 Berlin, Germany. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a uniqueness result for Gibbs point processes with interactions that come from a non-negative pair potential; in particular, we provide an explicit uniqueness region in terms of activity z and inverse temperature 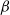$\beta$ . The technique used relies on applying to the continuous setting the classical Dobrushin criterion. We also present a comparison to the two other uniqueness methods of cluster expansion and disagreement percolation, which can also be applied for this type of interaction.

Keywords

Gibbs point processDLR equationsuniquenessDobrushin criterioncluster expansiondisagreement percolation

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 541 - 555
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belitsky, V. and Pechersky, E. A. (2002). Uniqueness of Gibbs state for non-ideal gas in $\mathbb{R}^d$ : The case of multibody interaction. J. Stat. Phys. 106, 931–955.CrossRefGoogle Scholar
Chayes, J. T., Chayes, L. and Kotecký, R. (1995). The analysis of the Widom–Rowlinson model by stochastic geometric methods. Commun. Math. Phys. 172, 551–569.CrossRefGoogle Scholar
Daley, D. J. (1974). Various concepts of orderliness for point-processes. In Stochastic Geometry (A Tribute to the Memory of Rollo Davidson), eds R. Davidson, D. G. Kendall and E. F. Harding, Wiley, London, pp. 148–161.Google Scholar
Daley, D. J. and Vere-Jones, D. (1988). An Introduction to the Theory of Point Processes. Springer, New York.Google Scholar
Dereudre, D. (2009). The existence of Quermass-interaction processes for nonlocally stable interaction and non-bounded convex grains. Adv. Appl. Prob. 41, 664–681.CrossRefGoogle Scholar
Dereudre, D. (2019). Introduction to the theory of Gibbs point processes. In Stochastic Geometry: Modern Research Frontiers, ed D. Coupier (Lect. Notes Math. 2237). Springer, Berlin, pp. 181–229.CrossRefGoogle Scholar
Dereudre, D., Drouilhet, R. and Georgii, H. O. (2012). Existence of Gibbsian point processes with geometry-dependent interactions. Prob. Theory Relat. Fields 153, 643–670.CrossRefGoogle Scholar
Dereudre, D. and Houdebert, P. (2019). Phase transition for continuum Widom–Rowlinson model with random radii. J. Stat. Phys. 174, 56–76.CrossRefGoogle Scholar
Dereudre, D. and Vasseur, T. (2020). Existence of Gibbs point processes with stable infinite range interaction. J. Appl. Prob. 57, 775–791.CrossRefGoogle Scholar
Dobrushin, R. L. (1968). The description of a random field by means of conditional probabilities and conditions of its regularity. Theory Prob. Appl. 13, 197–224.CrossRefGoogle Scholar
Dobrushin, R. L., and Pecherski, E. A. (1983). A criterion of the uniqueness of Gibbsian fields in the non-compact case. In Probability Theory and Mathematical Statistics, eds J. V. Prokhorov and K. ItÔ (Lect. Notes Math. 1021). Springer, Berlin, pp. 97–110.CrossRefGoogle Scholar
Ellis, S. P. (1991). Density estimation for point processes. Stoch. Process. Appl. 39, 345–358.CrossRefGoogle Scholar
Faris, W. G. (2008). A connected graph identity and convergence of cluster expansions. J. Math. Phys. 49, 113302.CrossRefGoogle Scholar
Fernández, R. and Procacci, A. (2007). Cluster expansion for abstract polymer models: New bounds from an old approach. Commun. Math. Phys. 274, 123–140.CrossRefGoogle Scholar
Fernández, R., Procacci, A. and Scoppola, B. (2007). The analyticity region of the hard sphere gas: Improved bounds. J. Stat. Phys. 128, 1139–1143.CrossRefGoogle Scholar
Georgii, H.-O. (1979). Canonical Gibbs Measures (Lect. Notes Math. 760). Springer, Berlin.CrossRefGoogle Scholar
Georgii, H.-O. (2011). Gibbs Measures and Phase Transitions, 2nd edn (Studies Math. 9). de Gruyter, Berlin.CrossRefGoogle Scholar
Georgii, H. O., Häggström, O. and Maes, C. (2001). The random geometry of equilibrium phases. In Phase Transitions and Critical Phenomena, Vol. 18, eds C. Domb and J. Lebowitz. Academic Press, New York, pp. 1–142.CrossRefGoogle Scholar
Hofer-Temmel, C. and Houdebert, P. (2019). Disagreement percolation for Gibbs ball models. Stoch. Process. Appl. 129, 3922–3940.CrossRefGoogle Scholar
Jansen, S. (2019). Cluster expansions for Gibbs point processes. Adv. Appl. Prob. 51, 1129–1178.CrossRefGoogle Scholar
Lanford, O. E. and Ruelle, D. (1969). Observables at infinity and states with short range correlations in statistical mechanics. Commun. Math. Phys. 13, 194–215.CrossRefGoogle Scholar
Last, G. and Penrose, M. (2017). Lectures on the Poisson Process. Cambridge University Press.CrossRefGoogle Scholar
Lebowitz, J. L. and Martin-Löf, A. (1972). On the uniqueness of the equilibrium state for Ising spin systems. Commun. Math. Phys. 25, 276–282.CrossRefGoogle Scholar
Malyshev, V. A. (1980). Cluster expansion in lattice models of statistical physics and the quantum theory of fields. Russ. Math. Surv. 35, 1–62.CrossRefGoogle Scholar
Malyshev, V. A. and Minlos, R. A. (1991). Gibbs Random Fields (Math. Appl. 44), Springer, Berlin.Google Scholar
Mayer, J. E. (1937). The statistical mechanics of condensing systems. I. J. Chem. Phys. 5, 67–73.CrossRefGoogle Scholar
Michelen, M. and Perkins, W. (2020). Analyticity for classical gasses via recursion. Preprint, arXiv:2008.00972.Google Scholar
Nehring, B., Poghosyan, S. and Zessin, H. (2013). On the construction of point processes in statistical mechanics. J. Math. Phys. 54, 063302.CrossRefGoogle Scholar
Pechersky, E. A. and Zhukov, Yu. (1999). Uniqueness of Gibbs state for nonideal gas in $\mathbb{R}^d$ : The case of pair potentials. J. Stat. Phys. 97, 145–172.CrossRefGoogle Scholar
Peierls, R. (1936). On Ising’s model of ferromagnetism. Math. Proc. Camb. Phil. Soc. 32, 477–481.CrossRefGoogle Scholar
Penrose, M. D. (1996). Continuum percolation and Euclidean minimal spanning trees in high dimensions. Ann. Appl. Prob. 6, 528–544.CrossRefGoogle Scholar
Poghosyan, S. and Ueltschi, D. (2009). Abstract cluster expansion with applications to statistical mechanical systems. J. Math. Phys. 50, 53509.CrossRefGoogle Scholar
Quintanilla, J., Torquato, S. and Ziff, R. M. (2000). Efficient measurement of the percolation threshold for fully penetrable discs. J. Phys. A. Math. Gen. 33, L399–L407.CrossRefGoogle Scholar
Rebenko, A. (2013). Cell gas model of classical statistical systems. Rev. Math. Phys. 25, 1330006.CrossRefGoogle Scholar
Resnick, S. (2014). A Probability Path. Birkhäuser, Basel.CrossRefGoogle Scholar
Rœlly, S. and Zass, A. (2020). Marked Gibbs point processes with unbounded interaction: An existence result. J. Stat. Phys. 179, 972–996.CrossRefGoogle Scholar
Ruelle, D. (1969). Statistical Mechanics: Rigorous Results. W. A. Benjamin, New York.Google Scholar
Ruelle, D. (1970). Superstable interactions in classical statistical mechanics. Commun. Math. Phys. 18, 127–159.CrossRefGoogle Scholar
Ruelle, D. (1971). Existence of a phase transition in a continuous classical system. Phys. Rev. Lett. 27, 1040–1041.CrossRefGoogle Scholar
Schuhmacher, D. (2005). Upper bounds for spatial point process approximations. Ann. Appl. Prob. 15, 615–651.CrossRefGoogle Scholar
Strauss, D. J. (1975). A model for clustering. Biometrika 62, 467–475.CrossRefGoogle Scholar
van den Berg, J. (1993). A uniqueness condition for Gibbs measures, with application to the 2-dimensional Ising antiferromagnet. Commun. Math. Phys. 152, 161–166.CrossRefGoogle Scholar
van den Berg, J. and Maes, C. (1994). Disagreement percolation in the study of Markov fields. Ann. Prob. 22, 749–763.Google Scholar