No CrossRef data available.
Article contents
An efficient method for generating a discrete uniform distribution using a biased random source
Published online by Cambridge University Press: 07 March 2023
Abstract
We present an efficient algorithm to generate a discrete uniform distribution on a set of p elements using a biased random source for p prime. The algorithm generalizes Von Neumann’s method and improves the computational efficiency of Dijkstra’s method. In addition, the algorithm is extended to generate a discrete uniform distribution on any finite set based on the prime factorization of integers. The average running time of the proposed algorithm is overall sublinear: 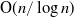 $\operatorname{O}\!(n/\log n)$.
$\operatorname{O}\!(n/\log n)$.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust



