Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T06:05:01.472Z Has data issue: false hasContentIssue false
  • English
  • Français

An averaging process on hypergraphs

Part of: Markov processes

Published online by Cambridge University Press:  29 March 2022

Sam Spiro Open the ORCID record for Sam Spiro [Opens in a new window]
Sam Spiro*
Affiliation:
University of California, San Diego
*
*Postal address: 9500 Gilman Dr, La Jolla, CA 92093. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the following iterated process on a hypergraph H. Each vertex v starts with some initial weight 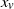$x_v$ . At each step, uniformly at random select an edge e in H, and for each vertex v in e replace the weight of v by the average value of the vertex weights over all vertices in e. This is a generalization of an interactive process on graphs which was first introduced by Aldous and Lanoue. In this paper we use the eigenvalues of a Laplacian for hypergraphs to bound the rate of convergence for this iterated averaging process.

Keywords

Markov chainspectral gap

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.)
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 495 - 504
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acemoğlu, D., Como, G., Fagnani, F. and Ozdaglar, A. (2013). Opinion fluctuations and disagreement in social networks. Math. Operat. Res. 38, 1–27.CrossRefGoogle Scholar
Aldous, D. et al. (2012). A lecture on the averaging process. Prob. Surv. 9, 90–102.CrossRefGoogle Scholar
Ben-Naim, E., Krapivsky, P. L. and Redner, S. (2003). Bifurcations and patterns in compromise processes. Physica D 183, 190–204.10.1016/S0167-2789(03)00171-4CrossRefGoogle Scholar
Brouwer, A. E. and Haemers, W. H. (2011). Spectra of Graphs. Springer, New York.Google Scholar
Butler, S. and Chung, F. (2006). Spectral graph theory. In Handbook of Linear Algebra, 2nd edn, ed. Hogben, L.. Chapman and Hall/CRC, London, p. 47–1.Google Scholar
Chatterjee, S., Diaconis, P., Sly, A. and Zhang, L. (2020). A phase transition for repeated averages. Preprint, arXiv:1911.02756.Google Scholar
Chatterjee, S. and Seneta, E. (1977). Towards consensus: Some convergence theorems on repeated averaging. J. Appl. Prob. 14, 89–97.CrossRefGoogle Scholar
Chung, F. (1993). The Laplacian of a hypergraph. In Expanding Graphs (DIMACS Series Discr. Math. Theoret. Comp. Sci. 10), ed. Friedman, J.. American Mathematical Society, Providence, RI, pp. 21–36.10.1090/dimacs/010/03CrossRefGoogle Scholar
Diaconis, P. and Saloff-Coste, L. (1993). Comparison techniques for random walk on finite groups. Ann. Prob. 2131–2156.10.1214/aop/1176989013CrossRefGoogle Scholar
Durrett, R. (2019). Probability: Theory and Examples (Camb. Ser. Statist. Prob. Math. 49). Cambridge University Press.Google Scholar
Feller, W. (2008). An Introduction to Probability Theory and its Applications, Vol. 2. John Wiley, New York.Google Scholar
Feng, K. et al. (1996). Spectra of hypergraphs and applications. J. Num. Theory 60, 1–22.10.1006/jnth.1996.0109CrossRefGoogle Scholar
Lu, L. and Peng, X. (2011). High-ordered random walks and generalized Laplacians on hypergraphs. In Proc. Int. Workshop Algorithms and Models for the Web Graph, eds. A. Frieze, P. Horn and P. PraŁat. Springer, New York, pp. 14–25.10.1007/978-3-642-21286-4_2CrossRefGoogle Scholar
Olshevsky, A. and Tsitsiklis, J. N. (2009). Convergence speed in distributed consensus and averaging. SIAM J. Control Optim. 48, 33–55.10.1137/060678324CrossRefGoogle Scholar
Rodríguez, J. A. (2002). On the Laplacian eigenvalues and metric parameters of hypergraphs. Linear Multilinear Algebra 50, 1–14.CrossRefGoogle Scholar
Shah, D. (2007). Gossip algorithms. Found. Trends Netw. 3, 1–125.10.1561/1300000014CrossRefGoogle Scholar