Article contents
An asymptotic result in traffic theory
Published online by Cambridge University Press: 14 July 2016
Extract
In problems of traffic theory, we are frequently concerned with the queues of vehicles which form at an intersection. A standard model is the vehicle queue whose length is increased during unit time intervals [t, t + 1) by non-negative integer inputs 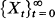 which form a sequence of i.i.d. or Markovian random variables; see Gani (1970) and Lehoczky ((1969), (1971)). The output from the queue at the end of each unit of time is one vehicle if the queue is non-empty, and no vehicle if there are none waiting.
which form a sequence of i.i.d. or Markovian random variables; see Gani (1970) and Lehoczky ((1969), (1971)). The output from the queue at the end of each unit of time is one vehicle if the queue is non-empty, and no vehicle if there are none waiting.
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1971
References
- 3
- Cited by


