Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T23:31:37.153Z Has data issue: false hasContentIssue false
  • English
  • Français

Age-dependent minimal repair

Published online by Cambridge University Press:  14 July 2016

Henry W. Block ,
Wagner S. Borges  and
Thomas H. Savits
Henry W. Block*
Affiliation:
University of Pittsburgh
Wagner S. Borges*
Affiliation:
Universidade de São Paulo
Thomas H. Savits*
Affiliation:
University of Pittsburgh
*
∗Postal address: Department of Mathematics and Statistics, University of Pittsburgh, Pittsburgh, PA 15260, USA.
∗∗Postal address: Instituto de Matemática e Estatística, Universidade de São Paulo, Caixa Postal 20570, Ag Iguatemi, 05508 São Paulo SP, Brazil.
∗∗∗Postal address: Department of Mathematics and Statistics, University of Pittsburgh, Pittsburgh, PA 15260, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

A stochastic model is developed to describe the operation in time of the following maintained system setting. A piece of equipment is put in operation at time 0. Each time it fails, a maintenance action is taken which, with probability p(t), is a complete repair or, with probability q(t)=1– p(t), is a minimal repair, where t is the age of the equipment in use at the failure time. It is assumed that complete repair restores the equipment to its good as new condition, that minimal repair restores the equipment to its condition just prior to failure and that both maintenance actions take negligible time.

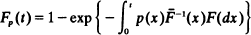If the equipment's life distribution F is a continuous function, the successive complete repair times are shown to be a renewal process with interarrival distribution for t ≧ 0. Preservation and monotone properties of the model extending the results of Brown and Proschan (1983) are obtained.

Keywords

MINIMAL REPAIRLIFE DISTRIBUTIONSRENEWAL PROCESSES
Type
Research Papers
Information
Journal of Applied Probability , Volume 22 , Issue 2 , June 1985 , pp. 370 - 385
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by Conselho Nacional de Desenvolvimento Cientifico e Tecnológico (CNPq), Processo No 200175–81.

Supported by ONR Contract N00014–76-C-0839.

References

Ascher, H. and Feingold, H. (1979) Comments on ‘Models for reliability of repaired equipment’. IEEE Trans. Reliability R-19, 119.CrossRefGoogle Scholar
Balaban, H. S. and Singpurwalla, N. D. (1981) The stochastic characterization of a sequence of life lengths under minimal repair actions. Technical Report, Serial No T-443, School of Engineering and Applied Sciences, George Washington University.Google Scholar
Blumenthal, S., Greenwood, J. A. and Herbach, L. H. (1976) A comparison of the bad as old and superimposed renewal models. Management Sci. 23, 280–285.Google Scholar
Brown, M. (1980) Bounds, inequalities and monotonicity properties for some specialized renewal processes. Ann. Prob. 8, 227–240.CrossRefGoogle Scholar
Brown, M. and Proschan, F. (1983) Imperfect repair. J. Appl. Prob. 20, 851–859.Google Scholar
Çinlar, E. (1975) Introduction to Stochastic Processes. Prentice Hall, New York.Google Scholar
Neveu, J. (1965) Mathematical Foundations of the Calculus of Probability. Holden Day, San Francisco.Google Scholar
Savits, T. H. (1976) An age dependent model with parental survival. Ann. Prob. 4, 382–392.Google Scholar