Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T03:05:51.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Survival under the pure birth shock model

Published online by Cambridge University Press:  14 July 2016

Bengt Klefsjö
Bengt Klefsjö*
Affiliation:
University of Luleå
*
∗Postal address: Department of Mathematics, University of Luleå, S-951 87 Luleå, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

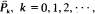Suppose that a device is subjected to shocks and that denotes the probability of surviving k shocks. Then 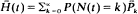is the probability that the device will survive beyond t, where 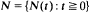is the counting process which governs the arrival of shocks. A-Hameed and Proschan (1975) considered the survival function H(t) under what they called the pure birth shock model. In this paper we shall prove that 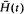is IFRA and DMRL under conditions which differ from those used by A-Hameed and Proschan (1975).

Keywords

SHOCK MODELBIRTH PROCESSSURVIVAL FUNCTIONVARIATION DIMINISHING PROPERTYTOTAL POSITIVITYIFRADFRADMRLIMRL
Type
Short Communications
Information
Journal of Applied Probability , Volume 18 , Issue 2 , June 1981 , pp. 554 - 560
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A-Hameed, M. S. and Proschan, F. (1973) Nonstationary shock models. Stoch Proc. Appl. 1, 383–404.Google Scholar
A-Hameed, M. S. and Proschan, F. (1975) Shock models with underlying birth process. J. Appl. Prob. 12, 18–28.Google Scholar
Barlow, R. E. and Proschan, F. (1975) Statistical Theory of Reliability and Life Testing. Probability Models. Holt, Rinehart and Winston, New York.Google Scholar
Block, H. W. and Savits, T. H. (1978) Shock models with NBUE survival. J. Appl. Prob. 15, 621–628.Google Scholar
Esary, J. D., Marshall, A. W. and Proschan, F. (1973) Shock models and wear processes. Ann. Prob. 1, 627–649.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. 1, 3rd edn. Wiley, New York.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. II, 2nd edn. Wiley, New York.Google Scholar
Karlin, S. (1968) Total Positivity, Vol. 1. Stanford University Press.Google Scholar
Karlin, S. and Proschan, F. (1960) Pólya type distributions of convolutions. Ann. Math. Statist. 31, 721–736.Google Scholar
Klefsjö, B. (1981) HNBUE survival under some shock models. Scand. J. Statist. 8, 39–47.Google Scholar