Article contents
Subgeometric ergodicity and β-mixing
Published online by Cambridge University Press: 16 September 2021
Abstract
It is well known that stationary geometrically ergodic Markov chains are 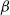 $\beta$
-mixing (absolutely regular) with geometrically decaying mixing coefficients. Furthermore, for initial distributions other than the stationary one, geometric ergodicity implies
$\beta$
-mixing (absolutely regular) with geometrically decaying mixing coefficients. Furthermore, for initial distributions other than the stationary one, geometric ergodicity implies 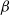 $\beta$
-mixing under suitable moment assumptions. In this note we show that similar results hold also for subgeometrically ergodic Markov chains. In particular, for both stationary and other initial distributions, subgeometric ergodicity implies
$\beta$
-mixing under suitable moment assumptions. In this note we show that similar results hold also for subgeometrically ergodic Markov chains. In particular, for both stationary and other initial distributions, subgeometric ergodicity implies 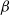 $\beta$
-mixing with subgeometrically decaying mixing coefficients. Although this result is simple, it should prove very useful in obtaining rates of mixing in situations where geometric ergodicity cannot be established. To illustrate our results we derive new subgeometric ergodicity and
$\beta$
-mixing with subgeometrically decaying mixing coefficients. Although this result is simple, it should prove very useful in obtaining rates of mixing in situations where geometric ergodicity cannot be established. To illustrate our results we derive new subgeometric ergodicity and 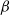 $\beta$
-mixing results for the self-exciting threshold autoregressive model.
$\beta$
-mixing results for the self-exciting threshold autoregressive model.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust
Footnotes
The supplementary material for this article can be found at http://doi.org/10.1017/jpr.2020.108.
References
- 2
- Cited by



