Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T20:34:55.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic models of damped vibrations

Part of: Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  14 July 2016

Maged Elshamy
Maged Elshamy*
Affiliation:
Alabama A&M University
*
∗Postal address: Department of Mathematics, Alabama A&M University, P.O. Box 326, Normal, Alabama 35762, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we study stochastic perturbations of partial differential equations describing forced-damped vibrations of a string. Two models of such stochastic disturbances are considered; one is triggered by an initial white noise, and the other is in the form of non-Gaussian random forcing. Let uε (t, x) be the displacement at time t of a point x on a string, where the time variable t ≧ 0, and the space variable 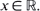. The small parameter ε controls the intensity of the random fluctuations. The random fields uε (t, x) are shown to satisfy a large deviations principle, and the random deviations of the unperturbed displacement function are analyzed as the noise parameter ε tends to zero.

Keywords

STOCHASTIC PERTURBATIONSDAMPED VIBRATIONSBROWNIAN SHEETRANDOM FIELDSDEVIATIONS

MSC classification

Primary: 60H15: Stochastic partial differential equations 60G60: Random fields
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 4 , December 1996 , pp. 1159 - 1168
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cabaña, E. M. (1991) A Gaussian process with parabolic covariance. J. Appl. Prob. 28, 898–902.CrossRefGoogle Scholar
Elshamy, M. (1995) Randomly perturbed vibrations. J. Appl. Prob. 32, 417–428.CrossRefGoogle Scholar
Freidlin, M. I. and Wentzell, A. D. (1984) Random Perturbations of Dynamical Systems. Springer, New York.CrossRefGoogle Scholar
Orsingher, E. (1984) Damped vibrations excited by white noise. Adv. Appl. Prob. 16, 562–584.CrossRefGoogle Scholar
Orsingher, E. (1989) On the maximum of Gaussian Fourier series emerging in the analysis of random vibrations. J. Appl. Prob. 26, 182–188.CrossRefGoogle Scholar
Walsh, J. B. (1984) An introduction to stochastic partial differential equations. école d'éte de Probabilitiés de Saint-Flour XIV. (Lecture Notes in Mathematics 1180). Springer, New York.Google Scholar