Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T19:48:39.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic asymptotic exponential stability of stochastic integral equations

Published online by Cambridge University Press:  14 July 2016

Chris P. Tsokos  and
M. A. Hamdan
Chris P. Tsokos
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia
M. A. Hamdan
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia
Get access Rights & Permissions [Opens in a new window]

Abstract

The object of this paper is to study the stochastic asymptotic exponential stability of a stochastic integral equation of the form

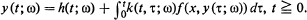
A random solution of the stochastic integral equation is considered to be a second order stochastic process satisfying the equation almost surely. The random solution, y(t, ω) is said to be. stochastically asymptotically exponentially stable if there exist some β > 0 and a γ > 0 such that 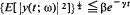for t∈ R+.

The results of the paper extend the results of Tsokos' generalization of the classical stability theorem of Poincaré-Lyapunov.

Keywords

RANDOM SOLUTION OF STOCHASTIC INTEGRAL EQUATIONSSTOCHASTIC ASYMPTOTIC EXPONENTIAL STABILITYPROBABILITY MEASURE SPACELp-SPACESADMISSIBILITY THEORYBANACH SPACESSTRONG CONVERGENCECONTRACTION MAPPING PRINCIPLE
Type
Research Papers
Information
Journal of Applied Probability , Volume 9 , Issue 1 , March 1972 , pp. 169 - 177
Copyright
Copyright © Applied Probability Trust 1972 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ahmed, N. U. (1969) A class of stochastic nonlinear integral equations on Lp spaces and its application to optimal control. Information and Control 14, 512–523.CrossRefGoogle Scholar
[2] Anderson, M. W. (1966) Stochastic Integral Equations. Ph.D. Dissertation, University of Tennessee.Google Scholar
[3] Bharucha-Reid, A. T. (1960) On random solutions of integral equations in Banach spaces. Trans. Second Prague Conf. Information Theory, Statistical Decision Function, and Random Processes, Academic Press, New York, 27–48.Google Scholar
[4] Bharucha-Reid, A. T. (1964) On the theory of random equations. Proc. Symp. Appl. Math. 16, 40–69. American Mathematical Society, Providence, Rhode Island.Google Scholar
[5] Distefano, N. (1968) A Volterra integral equation in the stability of some linear hereditary phenomena. J. Math. Anal. Appl. 23, 365–383.CrossRefGoogle Scholar
[6] Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
[7] Dunford, N. and Schwartz, J. (1958) Linear Operations, Part I. Interscience, New York.Google Scholar
[8] Fortet, R. (1956) Random distribution with applications to telephone engineering. Proc. Third Berkeley Symp. Math. Statist. and Prob. University of California Press, Berkeley, 81–88.Google Scholar
[9] Morozan, T. (1969) Stabilities Sistemelor cu Parametri Aleatori. Editura Academiei Republicii Socialiste Românio, Bucarest.Google Scholar
[10] Padgett, W. J. and Tsokos, C. P. (1971) On a stochastic integral equation of the Volterra type in telephone traffic theory. J. Appl. Prob. 8, 269–275.CrossRefGoogle Scholar
[11] Padgett, W. J. and Tsokos, C. P. (1971) On the existence of a solution of a stochastic integral equation in turbulence theory. J. Math. Phys. 12, 210–212.CrossRefGoogle Scholar
[12] Padgett, W. J. and Tsokos, C. P. (1970) On a semi-stochastic model arising in a biological system. Math. Biosciences 9, 105–117.CrossRefGoogle Scholar
[13] Padgett, W. J. and Tsokos, C. P. (1970) A stochastic model for chemotherapy: Computer simulation. Math. Biosciences 9, 119–133.CrossRefGoogle Scholar
[14] Tsokos, C. P. (1969) On a nonlinear differential system with a random parameter. Internat. Conf. on Systems Sciences, IEEE Proc., Honolulu, Hawaii.Google Scholar
[15] Tsokos, C. P. (1969) On some stochastic differential systems. IEEE Proc., Third Annual Princeton Conf. on Inf. of Sciences and Systems, 228–234.Google Scholar
[16] Tsokos, C. P. (1969) On the classical stability theorem of Poincaré-Lyapunov with a random parameter. Proc. Japan Acad. 45, 780–785.Google Scholar
[17] Tsokos, C. P. and Hamdan, M. A. (1970) Stochastic nonlinear integro-differential systems with time lag. J. Natur. Sci. and Math. 10, 293–303.Google Scholar