Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T22:07:51.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Some central limit analogues for supercritical Galton-Watson processes

Published online by Cambridge University Press:  14 July 2016

C. C. Heyde
C. C. Heyde*
Affiliation:
Australian National University
Get access Rights & Permissions [Opens in a new window]

Extract

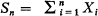It is possible to interpret the classical central limit theorem for sums of independent random variables as a convergence rate result for the law of large numbers. For example, if Xi, i = 1, 2, 3, ··· are independent and identically distributed random variables with EXi = μ, var Xi = σ2 < ∞ and then the central limit theorem can be written in the form This provides information on the rate of convergence in the strong law 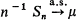as 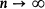. (“a.s.” denotes almost sure convergence.) It is our object in this paper to discuss analogues for the super-critical Galton-Watson process.

Type
Research Papers
Information
Journal of Applied Probability , Volume 8 , Issue 1 , March 1971 , pp. 52 - 59
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Gnedenko, B. V. and Kolmogorov, A. N. (1954) Limit Distributions for Sums of Independent Random Variables. Addison Wesley, Reading, Mass.Google Scholar
[2] Heyde, C. C. (1970) Extension of a result of Seneta for the super-critical Galton-Watson process. Ann. Math. Statist. 41, 739–742.CrossRefGoogle Scholar
[3] Heyde, C. C. (1970) A rate of convergence result for the super-critical Galton-Watson process. J. Appl. Prob. 7, 451–454.Google Scholar
[4] Kesten, H. and Stigum, B. P. (1966) A limit theorem for multi-dimensional Galton-Watson processes. Ann. Math. Statist. 37, 1211–1223.Google Scholar
[5] Lamperti, J. (1967) Limiting distributions for branching processes. Proc. 5th Berkeley Symposium on Math. Statist. and Prob. II, 225–241.Google Scholar
[6] Levinson, N. (1959) Limiting theorems for Galton-Watson branching process. Illinois J. Math. 3, 554–565.CrossRefGoogle Scholar
[7] Seneta, E. (1969) Functional equations and the Galton-Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar
[8] Stigum, B. P. (1966) A theorem on the Galton-Watson process. Ann. Math. Statist. 37, 695–698.Google Scholar