Article contents
Short-time behavior of solutions to Lévy-driven stochastic differential equations
Published online by Cambridge University Press: 12 January 2023
Abstract
We consider solutions of Lévy-driven stochastic differential equations of the form 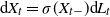 $\textrm{d} X_t=\sigma(X_{t-})\textrm{d} L_t$,
$\textrm{d} X_t=\sigma(X_{t-})\textrm{d} L_t$, 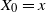 $X_0=x$, where the function
$X_0=x$, where the function  $\sigma$ is twice continuously differentiable and the driving Lévy process
$\sigma$ is twice continuously differentiable and the driving Lévy process 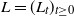 $L=(L_t)_{t\geq0}$ is either vector or matrix valued. While the almost sure short-time behavior of Lévy processes is well known and can be characterized in terms of the characteristic triplet, there is no complete characterization of the behavior of the solution X. Using methods from stochastic calculus, we derive limiting results for stochastic integrals of the form
$L=(L_t)_{t\geq0}$ is either vector or matrix valued. While the almost sure short-time behavior of Lévy processes is well known and can be characterized in terms of the characteristic triplet, there is no complete characterization of the behavior of the solution X. Using methods from stochastic calculus, we derive limiting results for stochastic integrals of the form 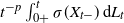 $t^{-p}\int_{0+}^t\sigma(X_{t-})\,\textrm{d} L_t$ to show that the behavior of the quantity
$t^{-p}\int_{0+}^t\sigma(X_{t-})\,\textrm{d} L_t$ to show that the behavior of the quantity 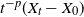 $t^{-p}(X_t-X_0)$ for
$t^{-p}(X_t-X_0)$ for 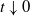 $t\downarrow0$ almost surely reflects the behavior of
$t\downarrow0$ almost surely reflects the behavior of 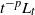 $t^{-p}L_t$. Generalizing
$t^{-p}L_t$. Generalizing 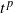 $t^{{\kern1pt}p}$ to a suitable function
$t^{{\kern1pt}p}$ to a suitable function 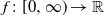 $f\colon[0,\infty)\rightarrow\mathbb{R}$ then yields a tool to derive explicit law of the iterated logarithm type results for the solution from the behavior of the driving Lévy process.
$f\colon[0,\infty)\rightarrow\mathbb{R}$ then yields a tool to derive explicit law of the iterated logarithm type results for the solution from the behavior of the driving Lévy process.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by



