Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T06:25:30.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Saddlepoint expansions for conditional distributions

Published online by Cambridge University Press:  14 July 2016

Ib M. Skovgaard
Ib M. Skovgaard*
Affiliation:
Royal Veterinary and Agricultural University, Copenhagen
*
∗Postal address: Royal Veterinary and Agricultural University, Department of Mathematics, Thorvaldsensvej 40, DK-1871 Frederiksberg C, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

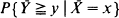A saddlepoint expansion is given for conditional probabilities of the form where 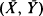is an average of n independent bivariate random vectors. A more general version, corresponding to the conditioning on a p – 1-dimensional linear function of a p-dimensional variable is also included. A separate formula is given for the lattice case. The expansion is a generalization of the Lugannani and Rice (1980) formula, which reappears if 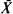and 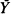are independent. As an example an approximation to the hypergeometric distribution is derived.

Keywords

CONDITIONAL PROBABILITYHYPERGEOMETRIC DISTRIBUTIONLATTICE VARIABLETAIL PROBABILITYUNIFORM SADDLEPOINT EXPANSION
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 4 , December 1987 , pp. 875 - 887
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barndorff-Nielsen, O. and Cox, O. R. (1979) Edgeworth and saddle-point approximations with statistical applications. J.R. Statist. Soc. B 41, 279–312.Google Scholar
Bleistein, N. (1966) Uniform asymptotic expansions of integrals with stationary point near algebraic singularity. Comm. Pure Appl. Math. 19, 353–370.CrossRefGoogle Scholar
Daniels, H. E. (1954) Saddlepoint approximations in statistics. Ann. Math. Statist. 25, 631–650.Google Scholar
Daniels, H. E. (1987) Tail probability approximations. Internat Statist. Rev. 55, 37–48.Google Scholar
Esscher, F. (1932) On the probability function in the collective theory of risk. Skand. Akt. Tidsskr. 15, 175–195.Google Scholar
Lugannani, R. and Rice, S. O. (1980) Saddlepoint approximation for the distribution of the sum of independent random variables. Adv. Appl. Prob. 12, 475–490.CrossRefGoogle Scholar
Molenaar, W. (1970) Approximations to the Poisson, Binomial and Hypergeometric Distribution Functions. Mathematical Centre Tracts, No. 31. Mathematisch Centrum, Amsterdam.Google Scholar
Olver, F. W. J. (1974) Asymptotics and Special Functions. Academic Press, New York.Google Scholar
Robinson, J. (1982) Saddlepoint approximation for permutation tests and confidence intervals. J.R. Statist. Soc. B 44, 91–101.Google Scholar
Temme, N. M. (1982) The uniform asymptotic expansion of integrals related to cumulative distribution functions. Siam J. Math. Anal. 13, 239–253.CrossRefGoogle Scholar