Published online by Cambridge University Press: 14 July 2016
Saddlepoint approximations are derived for the conditional cumulative distribution function and density of 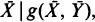 where
where 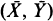 is the sample mean of n i.i.d. bivariate random variables and g(x, y) is a non-linear function. The relative error of order O(n–1) is retained. The results extend the important work of Skovgaard (1987), and are useful in conditional inference, especially in the case of small or moderate sample sizes. Generalizations to higher-dimensional random vectors are also discussed. Some examples are demonstrated.
is the sample mean of n i.i.d. bivariate random variables and g(x, y) is a non-linear function. The relative error of order O(n–1) is retained. The results extend the important work of Skovgaard (1987), and are useful in conditional inference, especially in the case of small or moderate sample sizes. Generalizations to higher-dimensional random vectors are also discussed. Some examples are demonstrated.