Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T14:57:50.773Z Has data issue: false hasContentIssue false
  • English
  • Français

A Poisson limit theorem for weakly exchangeable events

Published online by Cambridge University Press:  14 July 2016

G. K. Eagleson
G. K. Eagleson*
Affiliation:
University of Cambridge
*
∗Postal address: Statistical Laboratory, 16 Mill Lane, Cambridge CB2 1SB, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Y1, Y2, · ·· be a sequence of independent, identically distributed random variables, g some symmetric 0–1 function of m variables and set 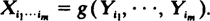Silverman and Brown (1978) have shown that under certain conditions the statistic 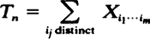is asymptotically distributed as a Poisson random variable. They then use this result to derive limit distributions for various statistics, useful in the analysis of spatial data. In this paper, it is shown that Silverman and Brown's theorem holds under much weaker assumptions; assumptions which involve only the symmetry of the joint distributions of the Xil…im.

Keywords

LIMIT THEOREMPOISSON DISTRIBUTIONU-STATISTICSWEAKLY EXCHANGEABLE RANDOM VARIABLES
Type
Research Papers
Information
Journal of Applied Probability , Volume 16 , Issue 4 , December 1979 , pp. 794 - 802
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, T. C. (1978) A martingale approach to the Poisson convergence of simple point processes. Ann. Prob. 6, 615–628.Google Scholar
Brown, T. C. and Silverman, B. W. (1979) Rates of Poisson convergence for U-statistics. J. Appl. Prob. 16, 428–432.Google Scholar
Eagleson, G. K. and Webber, N. C. (1978) Limit theorems for weakly exchangeable arrays. Math. Proc. Camb. Phil. Soc. 84, 123–130.Google Scholar
Freedman, D. (1974) The Poisson approximation for dependent events. Ann. Prob. 2, 256–269.CrossRefGoogle Scholar
Kaplan, N. (1977) Two applications of a Poisson approximation for dependent events. Ann. Prob. 5, 787–794.Google Scholar
Kendall, D. G. (1967) On finite and infinite sequences of exchangeable events. Studia Sci. Math. Hungar. 2, 319–327.Google Scholar
Ridler-Rowe, C. J. (1967) On two problems on exchangeable events. Studia Sci. Math. Hungar. 2, 415–418.Google Scholar
Ripley, B. D. (1977) Modelling spatial patterns. J. R. Statist. Soc. B 39, 172–212.Google Scholar
Serfling, R. J. (1975) A general Poisson approximation theorem. Ann. Prob. 3, 726–731.CrossRefGoogle Scholar
Silverman, B. W. (1976) Limit theorems for dissociated random variables. Adv. Appl. Prob. 8, 806–819.Google Scholar
Silverman, B. W. and Brown, T. C. (1978) Short distances, flat triangles and Poisson limits. J. Appl. Prob. 15, 815–825.Google Scholar