Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T07:19:40.001Z Has data issue: false hasContentIssue false
  • English
  • Français

On the matrix occurring in a linear search problem

Published online by Cambridge University Press:  14 July 2016

R. M. Phatarfod
R. M. Phatarfod*
Affiliation:
Monash University
*
∗Postal address: Department of Mathematics, Monash University, Clayton, VIC 3168, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

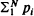In this paper we consider the Markov chain formed by the operation of the move-to-front scheme. We show that the eigenvalues of the transition probability matrix are of the form pi, pi + pj, ···, where pi is the probability of selecting the ith item and N is the number of items; further, that the multiplicity of the eigenvalues of the form Σpi where the summation is over m items is equal to the number of permutations of N – m objects, ordered in some way, such that no object is in its natural position. Finally, we show that the Markov chain is lumpable – many times over.

Keywords

EIGENVALUESMATCHING PROBLEMSLUMPABILITY
Type
Research Papers
Information
Journal of Applied Probability , Volume 28 , Issue 2 , June 1991 , pp. 336 - 346
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bitner, J. R. (1979) Heuristics that dynamically organize data structures. SIAM J. Computing 8, 82–110.Google Scholar
Burville, P. J. and Kingman, J. F. C. (1973) On a model for storage and search. J. Appl. Prob. 10, 697–701.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications. Vol. 1, 3rd edn. Wiley, New York.Google Scholar
Gonnet, G. H., Munro, J. I. and Suwanda, H. (1981) Exegesis of self-organizing linear search. SIAM J. Computing 10, 613–637.Google Scholar
Hendricks, W. J. (1972) The stationary distribution of an interesting Markov chain. J. Appl. Prob. 9, 231–233.Google Scholar
Hendricks, W. J. (1976) An account of self organizing systems. SIAM J. Computing 5, 715–723.Google Scholar
Kan, Y. C. and Ross, S. M. (1980) Optimal list order under partial memory constraints. J. Appl. Prob. 17, 1004–1015.Google Scholar
Kemeny, J. G. and Snell, J. L. (1960) Finite Markov Chains. Van Nostrand, N.J.Google Scholar
Mccabe, J. (1965) On serial files with relocatable records. Operat. Res. 12, 601–618.Google Scholar
Moran, P. A. P. (1968) An Introduction to Probability Theory. Clarendon Press, Oxford.Google Scholar
Rivest, R. (1976) On self-organizing sequential search heuristics. Comm. ACM 19, 63–67.Google Scholar