Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kolchin, V. F.
1994.
Random graphs and systems of linear equations in finite fields.
Random Structures & Algorithms,
Vol. 5,
Issue. 1,
p.
135.
Creignou, Nadia
and
Daudé, Hervé
2003.
Smooth and sharp thresholds for random{k}-XOR-CNF satisfiability.
RAIRO - Theoretical Informatics and Applications,
Vol. 37,
Issue. 2,
p.
127.
Creignou, Nadia
and
Daudé, Hervé
2004.
Combinatorial sharpness criterion and phase transition classification for random CSPs.
Information and Computation,
Vol. 190,
Issue. 2,
p.
220.
Durocher, Stephane
Gunderson, David S.
Li, Pak Ching
and
Skala, Matthew
2015.
Cycle-maximal triangle-free graphs.
Discrete Mathematics,
Vol. 338,
Issue. 2,
p.
274.
Verzelen, Nicolas
and
Arias-Castro, Ery
2015.
Community detection in sparse random networks.
The Annals of Applied Probability,
Vol. 25,
Issue. 6,
Arman, Andrii
Gunderson, David S.
and
Tsaturian, Sergei
2016.
Triangle-free graphs with the maximum number of cycles.
Discrete Mathematics,
Vol. 339,
Issue. 2,
p.
699.
Stivala, Alex
2020.
Geodesic Cycle Length Distributions in Delusional and Other Social Networks.
Journal of Social Structure,
Vol. 21,
Issue. 1,
p.
35.
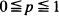 . Denote by γ n(p) the total number of cycles in the graph Γn(p). The main object of this paper is to prove that the limit distribution of γ n(λ /n) is a Poisson distribution with expectation
. Denote by γ n(p) the total number of cycles in the graph Γn(p). The main object of this paper is to prove that the limit distribution of γ n(λ /n) is a Poisson distribution with expectation 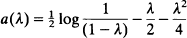 if n → ∞and 0 < λ< 1.
if n → ∞and 0 < λ< 1.