Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rathie, P. N.
1973.
Some characterization theorems for generalized measures of uncertainty and information.
Metrika,
Vol. 20,
Issue. 1,
p.
122.
1975.
On Measures of Information and their Characterizations.
Vol. 115,
Issue. ,
p.
219.
Autar, Ram
and
Soni, R. S.
1976.
Generalized inaccuracy and a coding theorem.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 84,
Issue. 5,
p.
204.
Kapur, J.N.
1983.
A Comparative Assessment of Various Measures of Entropy.
Journal of Information and Optimization Sciences,
Vol. 4,
Issue. 3,
p.
207.
Taneja, Inder Jeet
1989.
Vol. 76,
Issue. ,
p.
327.
Ilić, Velimir M.
and
Stanković, Miomir S.
2014.
A unified characterization of generalized information and certainty measures.
Physica A: Statistical Mechanics and its Applications,
Vol. 415,
Issue. ,
p.
229.
Rahimi, M.
2021.
A Spectral Representation for the Entropy of Topological Dynamical Systems.
Journal of Dynamical and Control Systems,
Vol. 27,
Issue. 3,
p.
573.
Ilić, V. M.
Korbel, J.
Gupta, S.
and
Scarfone, A. M.
2021.
An overview of generalized entropic forms(a).
Europhysics Letters,
Vol. 133,
Issue. 5,
p.
50005.
Kvalseth, Tarald O.
2022.
Entropies and Their Concavity and Schur-Concavity Conditions.
IEEE Access,
Vol. 10,
Issue. ,
p.
96006.
Singhal, Aakanksha
and
Sharma, D. K.
2022.
New Generalized ‘Useful’ Entropies using Weighted Quasi-Linear Mean for Efficient Networking.
Mobile Networks and Applications,
Vol. 27,
Issue. 3,
p.
1019.
Hosseinzadeh Dizaj, Mehran
2024.
Invariant measures of action of amenable groups and their entropy.
SSRN Electronic Journal,


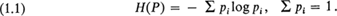
 and logarithms will be taken to the base
and logarithms will be taken to the base 