Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T07:23:34.211Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the inverse problem for reducible Markov chains

Published online by Cambridge University Press:  14 July 2016

A. O. Pittenger
A. O. Pittenger*
Affiliation:
University of Maryland, Baltimore County
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose a physical process is modelled by a Markov chain with transition probability 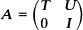on S1 ∪ S2, S1 denoting the transient states and S2 a set of absorbing states.

If v denotes the output distribution on S2, the question arises as to what input distributions (of raw materials) on S1 produce v. In this note we give an alternative to the formulation of Ray and Margo [2] and reduce the problem to one system of linear inequalities. An application to random walk is given and the equiprobability case examined in detail.

Keywords

DISCRETE-TIME MARKOV CHAINSHITTING TIMESINVERSE BOUNDARY VALUE PROBLEM
Type
Short Communications
Information
Journal of Applied Probability , Volume 14 , Issue 3 , September 1977 , pp. 621 - 625
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Balinski, M. L. (1961) An algorithm for finding all vertices of convex polyhedral sets. SIAM J. 9, 72–88.Google Scholar
[2] Ray, W. D. and Margo, F. (1976) The inverse problem in reducible Markov chains. J. Appl. Prob. 13, 49–56.CrossRefGoogle Scholar
[3] Ray, W. D. (1976) Specifying absorption probabilities for simple random walk. Stoch. Proc. Appl. 4, 243–252.CrossRefGoogle Scholar