Article contents
A model for a system subject to random shocks
Published online by Cambridge University Press: 14 July 2016
Abstract
A Markovian stochastic model for a system subject to random shocks is introduced. It is assumed that the shock arriving according to a Poisson process decreases the state of the system by a random amount. It is further assumed that the system is repaired by a repairman arriving according to another Poisson process if the state when he arrives is below a threshold α. Explicit expressions are deduced for the characteristic function of the distribution function of X(t), the state of the system at time t, and for the distribution function of X(t), if 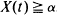 . The stationary case is also discussed.
. The stationary case is also discussed.
Keywords
MSC classification
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1993
Footnotes
Research has been supported by the Korea Science and Engineering Foundation (KOSEF), under Grant Number 913-0105-002-2.
References
- 4
- Cited by


