Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T16:38:10.746Z Has data issue: false hasContentIssue false
  • English
  • Français

Misspecified change-point estimation problem for a Poisson process

Part of: Parametric inference Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Ali S. Dabye  and
Yury A. Kutoyants
Ali S. Dabye*
Affiliation:
Université de N'Djamena
Yury A. Kutoyants*
Affiliation:
Université du Maine
*
1Postal address: Faculté des Sciences Exactes et Appliquées, Université de N'Djamena, BP 1027, N'Djamena, Chad. Email: [email protected]
2Postal address: Laboratoire de Statistique et Processus, Université du Maine, 72085 Le Mans, Cedex 9, France. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

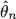Consider an inhomogeneous Poisson process X on [0, T] whose unknown intensity function ‘switches' from a lower function g∗ to an upper function h∗ at some unknown point θ∗. What is known are continuous bounding functions g and h such that g∗(t) ≤ g(t) ≤ h(t) ≤ h∗(t) for 0 ≤ t ≤ T. It is shown that on the basis of n observations of the process X the maximum likelihood estimate of θ∗ is consistent for n →∞, and also that 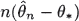converges in law and in pth moment to limits described in terms of the unknown functions g∗ and h∗.

Keywords

Inhomogeneous Poisson processchange-type problemparameter estimationmisspecified modelconsistencylimit distribution

MSC classification

Primary: 62F12: Asymptotic properties of estimators
Secondary: 60G55: Point processes
Type
Estimation problems
Information
Journal of Applied Probability , Volume 38 , Issue A: Probability, Statistics and Seismology , 2001 , pp. 122 - 130
Copyright
Copyright © Applied Probability Trust 2001 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Campillo, F., Kutoyants, Yu and Le Gland, F. A. (2000). Small noise asymptotics of the GLR test for off-line change detection in misspecified diffusion processes. Stochastics Stochastics Rep. 70, 109–129.CrossRefGoogle Scholar
Dab Ye, A. S. (1999). Estimation paramétrique pour un processus de Poisson de fonction d'intensité discontinue. Doctoral Thesis, Université du Maine.Google Scholar
Daley, D. J. and Vere-Jones, D. (1988). An Introduction to the Theory of Point Processes. Springer, New York.Google Scholar
Ibragimov, I. A. and Khasminskii, R. Z. (1981). Statistical Estimation: Asymptotic Theory. Springer, New York.CrossRefGoogle Scholar
Karr, A. F. (1991). Point Processes and Their Statistical Inference , 2nd edn. Marcel Dekker, New York.Google Scholar
Kutoyants, Yu. A. (1994). Identification of Dynamical Systems with Small Noise. Kluwer, Dordrecht.CrossRefGoogle Scholar
Kutoyants, Yu. A. (1998). Statistical Inference for Spatial Poisson Processes (Lecture Notes Statist. 134). Springer, New York.Google Scholar
Snyder, D. R. and Miller, M. I. (1991). Random Point Processes in Time and Space. Springer, New York.Google Scholar
Vere-Jones, D. (1982). On the estimation of frequency in point-process data. In Essays in Statistical Science (J. Appl. Probab. 19A), eds Gani, J. and Hannan, E. J., Applied Probability Trust, Sheffield, 383–394.Google Scholar