Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lamperti, John
1972.
Remarks on Maximal Branching Processes.
Theory of Probability & Its Applications,
Vol. 17,
Issue. 1,
p.
44.
Tautu, P.
1986.
Stochastic Spatial Processes.
Vol. 1212,
Issue. ,
p.
1.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Лебедев, Алексей Викторович
and
Lebedev, Alexey Viktorovich
2002.
Двойной показательный закон для максимальных ветвящихся процессов.
Дискретная математика,
Vol. 14,
Issue. 3,
p.
143.
Лебедев, Алексей Викторович
and
Lebedev, Alexey Viktorovich
2005.
Максимальные ветвящиеся процесы с неотрицательными значениями.
Теория вероятностей и ее применения,
Vol. 50,
Issue. 3,
p.
564.
Lebedev, A. V.
2006.
Maximal Branching Processes with Nonnegative Values.
Theory of Probability & Its Applications,
Vol. 50,
Issue. 3,
p.
482.
Лебедев, Алексей Викторович
and
Lebedev, Alexey Viktorovich
2009.
Асимптотика хвостов стационарных распределений максимальных ветвящихся процессов.
Теория вероятностей и ее применения,
Vol. 54,
Issue. 4,
p.
790.
Lebedev, A. V.
2010.
Tail Asymptotics for Stationary Distributions of Maximal Branching Processes.
Theory of Probability & Its Applications,
Vol. 54,
Issue. 4,
p.
699.
Lebedev, A. V.
2012.
Maximal branching processes with several types of particles.
Moscow University Mathematics Bulletin,
Vol. 67,
Issue. 3,
p.
97.
Aydogmus, Ozgur
Aydogmus, Ozgur
Ghosh, Arka P
Ghosh, Arka P
Ghosh, Sukumar
Ghosh, Sukumar
Roitershtein, Alexander
and
Roitershtein, Alexander
2014.
Coloured maximal branching process.
Теория вероятностей и ее применения,
Vol. 59,
Issue. 4,
p.
790.
Aydogmus, O.
Ghosh, A. P.
Ghosh, S.
and
Roitershtein, A.
2015.
Colored Maximal Branching Process.
Theory of Probability & Its Applications,
Vol. 59,
Issue. 4,
p.
663.
Bezborodov, Viktor
2021.
Non-triviality in a totally asymmetric one-dimensional Boolean percolation model on a half-line.
Statistics & Probability Letters,
Vol. 176,
Issue. ,
p.
109155.
Huillet, Thierry
and
Martinez, Servet
2022.
Revisiting John Lamperti's maximal branching process.
Stochastics,
Vol. 94,
Issue. 2,
p.
277.
Braun, Georg
2024.
Boolean percolation on digraphs and random exchange processes.
Journal of Applied Probability,
Vol. 61,
Issue. 3,
p.
755.
Bezborodov, Viktor
Di Persio, Luca
and
Kuchling, Peter
2024.
Explosion and non-explosion for the continuous-time frog model.
Stochastic Processes and their Applications,
Vol. 171,
Issue. ,
p.
104329.
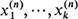 are independent random variables representing their respective numbers of offspring, then the (n + 1)th generation will contain max
are independent random variables representing their respective numbers of offspring, then the (n + 1)th generation will contain max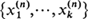 individuals rather than
individuals rather than 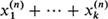 as in the branching case. Equivalently, the transition matrices Pij of the chains we will study are to be of the form
as in the branching case. Equivalently, the transition matrices Pij of the chains we will study are to be of the form
 where F(.) is the probability distribution function of a non-negative, integervalued random variable. The right-hand side of (1) is thus the probability that the maximum of i independent random variables distributed by F has the value j. Such a chain will be called a “maximal branching process”.
where F(.) is the probability distribution function of a non-negative, integervalued random variable. The right-hand side of (1) is thus the probability that the maximum of i independent random variables distributed by F has the value j. Such a chain will be called a “maximal branching process”.

