Article contents
Limiting results for arrays of binary random variables on rectangular lattices under sparseness conditions
Published online by Cambridge University Press: 14 July 2016
Abstract
In this article we give limiting results for arrays {Xij (m, n) (i, j) 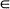 Dmn} of binary random variables distributed as particular types of Markov random fields over m x n rectangular lattices Dmn. Under some sparseness conditions which restrict the number of Xij (m, n)'s which are equal to one we show that the random variables (l = 1, ···, r)
Dmn} of binary random variables distributed as particular types of Markov random fields over m x n rectangular lattices Dmn. Under some sparseness conditions which restrict the number of Xij (m, n)'s which are equal to one we show that the random variables (l = 1, ···, r)
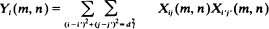 converge to independent Poisson random variables for 0 < d1 < d2 < · ·· < dr when m→∞ nd∞.
converge to independent Poisson random variables for 0 < d1 < d2 < · ·· < dr when m→∞ nd∞. 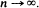 The particular types of Markov random fields considered here provide clustering (or repulsion) alternatives to randomness and involve several parameters. The limiting results are used to consider statistical inference for these parameters. Finally, a simulation study is presented which examines the adequacy of the Poisson approximation and the inference techniques when the lattice dimensions are only moderately large.
The particular types of Markov random fields considered here provide clustering (or repulsion) alternatives to randomness and involve several parameters. The limiting results are used to consider statistical inference for these parameters. Finally, a simulation study is presented which examines the adequacy of the Poisson approximation and the inference techniques when the lattice dimensions are only moderately large.
Keywords
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1979
Footnotes
Research partially supported by the National Science Foundation Grant No. MCS 77–03582.
References
- 8
- Cited by


