Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T20:29:08.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Les familles exponentielles statistiques invariantes par les groupes du cône et du paraboloide de révolution

Published online by Cambridge University Press:  14 July 2016

Gérard Letac
Get access Rights & Permissions [Opens in a new window]

Abstract

Statistical exponential families invariant with respect to the groups of the cone or the paraboloid of revolution are discussed. B(x, y) denotes the symmetric bilinear form on x0y0 – x1y1 – ·· ·– xdyd on ℝd+1, C denotes the cone of revolution in ℝd+1 {x; B(x,x) > 0 and x0 > 0}, and, for p > ½(d−1), μ p is the positive measure on ℝd+1 defined by its Laplace transform ⨍ exp (B(x,y))μp(dy) = (B(y,y))−p for y on C. More precisely, if p > ½ (d−1) one has 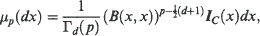and μ½(d−1) concentrated on the boundary ∂C. This paper studies the natural exponential families

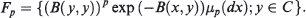
Type
Part 2 Probabilistic Methods
Information
Journal of Applied Probability , Volume 31 , Issue A , 1994 , pp. 71 - 95
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

Andersson, S. A. (1975) Invariant normal models. Ann. Statist. 3, 132–154.CrossRefGoogle Scholar
Artzner, Ph. Et Fourt, G. (1974) Lois gamma et bêta sur un cône convexe homogène. Applications à l'analyse multivariée. C. R. Acad. Sci. Paris. 278 A, 293–295.Google Scholar
Barndorff-Nielsen, O., Blaesild, P. Et Eriksen, P. S. (1989) Decomposition and Invariance of Measures, and Statistical Transformation Models. Lecture Notes in Statistics 58, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Casalis, M. (1990) Familles Exponentielles Naturelles Invariantes par un Groupe. Thèse, Université Paul Sabatier, Toulouse.Google Scholar
Deheuvels, R. (1981) Formes Quadratiques et Groupes Classiques. Presses Universitaires de France, Paris.Google Scholar
Dieudonne, J. et al. (1986) Abrégé d'Histoire des Mathématiques . Hermann, Paris.Google Scholar
Gindikin, S. G. (1964) Analysis on homogeneous domains. Russian Maths. Surveys 19, 1–89.Google Scholar
Gindikin, S. G. (1975) Invariant generalized functions in homogeneous domains. Funct. Anal. Appl. 9, 50–52.Google Scholar
Jensen, S. T. (1988) Covariance hypotheses which are linear in both the covariance and the inverse covariance. Ann. Statist. 16, 302–322.Google Scholar
Johnson, N. L. Et Kotz, S. (1972) Distributions in Statistics: Continuous Multivariate Distributions , Wiley, New York.Google Scholar
Jørgensen, B. (1987) Exponential dispersion models. J. R. Statist. Soc. B49, 127–162.Google Scholar
Letac, G. Et Mora, M. (1990) Natural exponential families with cubic variance functions. Ann. Statist. 18, 1–37.Google Scholar
Letac, G. (1989) A characterization of the Wishart exponential families by an invariance property. J. Theoret. Prob. 2, 71–86.CrossRefGoogle Scholar
Marsaglia, G. (1972) Choosing a point from the surface of a sphere. Ann. Math. Statist. 43, 645–646.CrossRefGoogle Scholar
Mora, M. (1986) Classification des fonctions-variance cubiques des familles exponentielles sur ℝ. C. R. Acad. Sci. Paris 302(I), 16, 582-591.Google Scholar
Morris, C. N. (1982) Natural exponential families with quadratic variance functions. Ann. Statist. 10, 568–576.Google Scholar
Muirhead, R. J. (1982) Aspects of Multivariate Statistical Theory. Wiley, New York.CrossRefGoogle Scholar
Perlman, M. D. (1987) Group symmetric covariance models, a discussion of Mark J. Servish ‘A review of multivariate analysis’. Statist. Sci. 2, 421–425.Google Scholar
Ribenboïm, P. (1972) L'Arithmétique des Corps. Hermann, Paris.Google Scholar
Watson, G. N. (1966) A Treatise on the Theory of Bessel Functions , 2nd edn. Cambridge University Press.Google Scholar