Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T05:24:24.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities with applications to percolation and reliability

Published online by Cambridge University Press:  14 July 2016

J. Van Den Berg  and
H. Kesten
J. Van Den Berg*
Affiliation:
Delft University of Technology
H. Kesten*
Affiliation:
Cornell University
*
∗Postal address: Department of Mathematics, Delft University of Technology, 2628 BL Delft, The Netherlands.
∗∗Postal address: Department of Mathematics, Cornell University, Ithaca, NY 14853, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

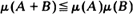A probability measure μ on ℝn+ is defined to be strongly new better than used (SNBU) if for all increasing subsets 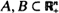. For n = 1 this is equivalent to being new better than used (NBU distributions play an important role in reliability theory). We derive an inequality concerning products of NBU probability measures, which has as a consequence that if μ1, μ2, ···, μn are NBU probability measures on ℝ+, then the product-measure μ = μ × μ2 × ··· × μn on ℝn+ is SNBU. A discrete analog (i.e., with N instead of ℝ+) also holds.

Applications are given to reliability and percolation. The latter are based on a new inequality for Bernoulli sequences, going in the opposite direction to the FKG–Harris inequality. The main application (3.15) gives a lower bound for the tail of the cluster size distribution for bond-percolation at the critical probability. Further applications are simplified proofs of some known results in percolation. A more general inequality (which contains the above as well as the FKG-Harris inequality) is conjectured, and connections with an inequality of Hammersley [12] and others ([17], [19] and [7]) are indicated.

Keywords

CORRELATION INEQUALITIESFKG INEQUALITYNEW BETTER THAN USED
Type
Research Papers
Information
Journal of Applied Probability , Volume 22 , Issue 3 , September 1985 , pp. 556 - 569
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ahlswede, R. and Daykin, D. E. (1979) Inequalities for a pair of maps S × S ? S with S a finite set. Math. Z. 165, 269–289.CrossRefGoogle Scholar
[2] Aizenman, M. and Newman, C. M. (1985) Tree graph inequalities and critical behavior in percolation models. J. Statist. Phys. Google Scholar
[3] Barlow, R. E. and Proschan, F. (1975) Statistical Theory of Life Testing and Probability Models. Holt, Rinehart and Winston, New York.Google Scholar
[4] Van Den Berg, J. (1985) To appear.Google Scholar
[5] Van Den Berg, J. and Fiebig, U. (1984) On a combinatorial conjecture concerning disjoint occurrences of events. Preprint.Google Scholar
[6] Broadbent, S. R. and Hammersley, J. M. (1957) Percolation processes. Proc. Camb. Phil. Soc. 53, 629–641; 642–645.Google Scholar
[7] Campanino, M. and Russo, L. (1985) An upper bound on the critical probability for the three-dimensional cubic lattice. Ann. Prob. 13.Google Scholar
[8] Dellacherie, C. and Meyer, P. A. (1978) Probabilities and Potential. North-Holland, Amsterdam.Google Scholar
[9] Durrett, R. (1984) Oriented percolation in two dimensions. Ann. Prob. 12.CrossRefGoogle Scholar
[10] Fortuin, C. M., Kasteleyn, P. W. and Ginibre, J. (1971) Correlation inequalities on some partially ordered sets. Commun. Math. Phys. 22, 89–103.Google Scholar
[11] Hammersley, J. M. (1957) Percolation processes. Lower bounds for the critical probability. Ann. Math. Statist. 28, 790–795.CrossRefGoogle Scholar
[12] Hammersley, J. M. (1961) Comparison of atom and bond percolation processes. J. Math. Phys. 2, 728–733.CrossRefGoogle Scholar
[13] Harris, T. E. (1960) A lower bound for the critical probability in a certain percolation process. Proc. Camb. Phil. Soc. 56, 13–20.CrossRefGoogle Scholar
[14] Kesten, H. (1982) Percolation Theory for Mathematicians. Birkhauser, Boston.Google Scholar
[15] Kesten, H. (1984) Aspects of first-passage percolation. St Flour Summer School in Probability.Google Scholar
[16] Marshall, A. W. and Shaked, M. (1982) A class of multivariate new better than used distributions. Ann. Prob. 10, 259–264.CrossRefGoogle Scholar
[17] Mcdiarmid, C. J. H. (1981) General percolation and random graphs. Adv. Appl. Prob. 13, 40–60.Google Scholar
[18] Mcdiarmid, C. J. H. (1983) General first-passage percolation. Adv. Appl. Prob. 15, 149–161.Google Scholar
[19] Rüschendorf, L. (1982) Comparison of percolation probabilities. J. Appl. Prob. 19, 864–868.Google Scholar
[20] Seymour, P. W. and Welsh, D. J. A. (1978) Percolation probabilities on the square lattice. Ann. Discrete Math. 3, 227–245.CrossRefGoogle Scholar