Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:27:09.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy and martingales in Markov chain models

Published online by Cambridge University Press:  14 July 2016

E. Seneta
Get access Rights & Permissions [Opens in a new window]

Abstract

The concept of entropy in models is discussed with particular reference to the work of P.A.P. Moran. For a vector-valued Markov chain {Xk} whose states are relative-frequency (proportion) tables corresponding to a physical mixing model of a number N of particles over n urns, the definition of entropy may be based on the usual information-theoretic concept applied to the probability distribution given by the expectation 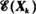. The model is used for a brief probabilistic assessment of the relationship between Boltzmann's Η-Theorem, the Ehrenfest urn model, and Poincaré's considerations on the mixing of liquids and card shuffling, centred on the property of an ultimately uniform distribution of a single particle. It is then generalized to the situation where the total number of particles fluctuates over time, and martingale results are used to establish convergence for .

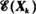Keywords

ENTROPYMARKOV CHAINSURN MODELSMARTINGALESFLUCTUATING POPULATION SIZE
Type
Part 6 — Stochastic Processes
Information
Journal of Applied Probability , Volume 19 , Issue A , 1982 , pp. 367 - 381
Copyright
Copyright © 1982 Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ash, R.B. (1972) Real Analysis and Probability. Academic Press, New York.Google Scholar
[2] Bernoulli, D. (1769) Disquisitiones analyticae de novo problemate conjecturale. Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae 14, pars 1, 3–25.Google Scholar
[3] Ehrenfest, P. and Ehrenfest, T. (1907) Über zwei bekannte Einwände gegen das Boltzmannsche H-Theorem. Phys. Z. 8, 311–314.Google Scholar
[4] Ewens, W.J. (1969) Population Genetics. Methuen, London.Google Scholar
[5] Feller, W. (1968) An Introduction to Probability Theory and its Applications , Vol. 1, 3rd edn. Wiley, New York.Google Scholar
[6] Fisher, R.A. (1958) The Genetical Theory of Natural Selection , 2nd edn. Dover, New York.Google Scholar
[7] Johnson, N.L. and Kotz, S. (1977) Urn Models and their Application. Wiley, New York.Google Scholar
[8] Kac, M. (1947) Random walk and the theory of Brownian motion. Amer. Math. Monthly 54, 369–391. Reprinted (1954); Selected Papers on Noise and Stochastic Processes , ed. Wax, N., Dover, New York, 295–317.Google Scholar
[9] Kac, M. (1959) Probability and Related Topics in Physical Sciences. Interscience, London.Google Scholar
[10] Kac, M. (1964) Probability. Scientific American 211 (September), 92–108.CrossRefGoogle Scholar
[11] Khinchin, A.I. (1957) Mathematical Foundations of Information Theory. Dover, New York.Google Scholar
[12] Kohlrausch, K.W.F. and Schrödinger, ?. (1926) Das Ehrenfestsche Modell der ?-Kurve. Phys. Z. 27, 306–313.Google Scholar
[13] Li, C.C. (1967) Genetic equilibrium under selection. Biometrics 23, 397–484.CrossRefGoogle ScholarPubMed
[14] Moran, P.A.P. (1959–1960) The survival of a mutant under selection, I and II. J. Austral. Math. Soc. 1, 121–126, 485–491.Google Scholar
[15] Moran, P.A.P. (1961) Entropy, Markov processes and Boltzmann's ?-Theorem. Proc. Camb. Phil. Soc. 57, 833–842.Google Scholar
[16] Moran, P.A.P. (1962) The Statistical Processes of Evolutionary Theory. Clarendon Press, Oxford.Google Scholar
[17] Moran, P.A.P. (1964) On the non-existence of adaptive topographies. Ann. Human Genet. 27, 383–393.CrossRefGoogle Scholar
[18] Neveu, J. (1965) Mathematical Foundations of the Calculus of Probability. Holden-Day, San Francisco.Google Scholar
[19] Poincaré, H. (1912) Calcul des Probabilités , deuxième édition. Gauthier–Villars, Paris.Google Scholar
[20] Seneta, ?. (1978) A relaxation view of a genetic problem. Adv. Appl. Prob. 10, 716–720.Google Scholar
[21] Sheynin, O.B. (1972) D. Bernoulli's work on probability. Rete 1, 273–299.Google Scholar
[22] Urban, F.M. (1932) Das Mischungsproblem des Daniel Bernoulli. Atti Del Congresso Internazionale Dei Matematici, Bologna , 1928, 6, 21–25.Google Scholar