Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T04:00:35.279Z Has data issue: false hasContentIssue false
  • English
  • Français

An invariance principle in k-dimensional extended renewal theory

Published online by Cambridge University Press:  14 July 2016

Attila Csenki
Attila Csenki*
Affiliation:
Universität Freiburg im Breisgau
*
∗ Postal address: Institut für Mathematische Stochastik der Albert–Ludwigs Universität, Hermann Herder Strasse 10, 78 Freiburg im Breisgau, West Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 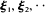·be a sequence of k -dimensional i.i.d. random vectors and define the first-passage times 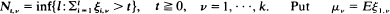for 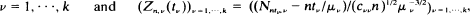where (cvτ)v, τ= 1,· ··,k is the covariance matrix of 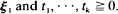In this paper the weak convergence of Zn in (D[0, ∞))k is proved under the assumption 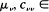(0,∞) for all v = 1, ···, k. We deduce the result from the Donsker invariance principle by means of Theorem 5.5 of Billingsley (1968). This method is also used to derive a limit theorem for the first-exit time Mn = min{Nnt 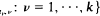for fixed t1,···, tk > 0. The second result is an extension of a theorem of Hunter (1974) whose method of proof applies only if Ρ (ξ1 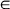[0,∞)k) = 1 and μ ν = tv for all v = 1, ···, k.

Keywords

EXTENDED RENEWAL THEORYWEAK CONVERGENCEINVARIANCE PRINCIPLEFUNCTION SPACE D[0,∞)
Type
Research Papers
Information
Journal of Applied Probability , Volume 16 , Issue 3 , September 1979 , pp. 567 - 574
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[2] Gut, A. (1973) A functional central limit theorem connected with extended renewal theory. Z. Wahrscheinlichkeitsth. 27, 123–129.Google Scholar
[3] Hunter, J. J. (1974) Renewal theory in two dimensions: asymptotic results. Adv. Appl. Prob. 6, 546–562.Google Scholar
[4] Lindvall, T. (1973) Weak convergence of probability measures and random functions in the function space D[0, 8). J. Appl. Prob. 10, 109–121.Google Scholar