Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T17:48:20.234Z Has data issue: false hasContentIssue false
  • English
  • Français

Performance of a new evaporative misting system based on photovoltaic/thermal and ventilation heat exchange in sow farms: a case study in Guangzhou, China

Published online by Cambridge University Press:  21 November 2024

Yue Xie ,
Qinghua Li ,
Hongqiang Ma Open the ORCID record for Hongqiang Ma [Opens in a new window] ,
Jiajun Wang  and
Shengxun Wang
Yue Xie
Affiliation:
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, China
Qinghua Li*
Affiliation:
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, China
Hongqiang Ma*
Affiliation:
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, China
Jiajun Wang
Affiliation:
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, China
Shengxun Wang
Affiliation:
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, China
*
Corresponding authors: Qinghua Li; Email: [email protected]; Hongqiang Ma; Email: [email protected]
Corresponding authors: Qinghua Li; Email: [email protected]; Hongqiang Ma; Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

In order to improve the regional applicability of existing evaporative misting systems, a new evaporative misting system based on photovoltaic/thermal and ventilation heat exchange is proposed for sow farms. Compared to traditional systems, the proposed system can help to improve their regional applicability and reduce their energy consumption. Meanwhile, its simulation model is constructed and the reliability is verified for its core equipment. The maximum error is less than 14.5% for the above models. Through simulation, the optimal regulation variable ranges in the proposed system are determined for mass flow rate of working fluid (MFWF) and misting power by analysing its operating characteristics. The results show that its optimal ranges of MFWF and misting power are 7245–9245 kg/h and 40–45 kW, respectively. The annual performance is further quantified and analysed under different load ratios for the proposed system in Guangzhou. It can be found that the annual exergy loss, heat exchange coefficient and solar energy benefits of the proposed system in Guangzhou are negatively correlated with load ratio, but its annual energy consumption and energy efficiency ratio are positively correlated. Meanwhile, the system performance and benefits are not significantly improved by increasing device investment and sow density when load ratio exceeds 120% in sow farms. The above conclusion can contribute to improving the existing evaporative misting systems in sow farms and guiding the operating regulation of the proposed system.

Keywords

annual operating modesannual performanceload ratiooptimal regulation variable ranges
Type
Modelling Animal Systems Research Paper
Information
The Journal of Agricultural Science , First View , pp. 1 - 14
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press

Introduction

The intensive pig farms have become the main trend in the development of pig industries (Ma et al., Reference Ma, Xie, Li, Zhang, Liu and Luo2023a, Reference Ma, Xie, Wang, Min, Luo and Cai2023b). Under high temperature conditions, sows suffer from heat stress, which significantly reduces their production performance (St-Pierre et al., Reference St-Pierre, Cobanov and Schnitkey2003; Liu et al., Reference Liu, Tai, Yao, Zhao and Shen2021). Therefore, regulating the indoor thermal environment is crucial for improving sow productivity (Johnson et al., Reference Johnson, Martin, Pohler and Stewart2016a, Reference Johnson, Sapkota and Lay J2016b). However, a significant amount of ventilation and energy are required to regulate the indoor temperature through mechanical ventilation systems in large-scale sow farms (Costantino et al., Reference Costantino, Fabrizio, Biglia, Cornale and Battaglini2016; Kupchuk and Telekalo, Reference Kupchuk and Telekalo2022). Moreover, during the regulation process of indoor temperature, large amounts of greenhouse gases are produced due to energy consumption (Nakomcic-Smaragdakis et al., Reference Nakomcic-Smaragdakis, Stajic, Cepic and Djuric2012). Therefore, developing energy-saving temperature regulation systems is an urgent need for pig industries.

In pig farms, there are many temperature regulation systems such as traditional ventilation systems (Tabase, Reference Tabase2019), ground source heat pump systems (Opderbeck et al., Reference Opderbeck, Keßler, Gordillio, Schrade, Piepho and Gallmann2020) and evaporative misting systems (Romanini et al., Reference Romanini, Tolon, Nääs and Moura2008). However, poor cooling effect and high energy consumption are the main problems of these systems (Ma et al., Reference Ma, Xie, Wang, Liu and Ding2023c, Reference Ma, Xie, Song, Liu, Luo and Wang2023d). It can be found that the energy consumption and ammonia concentration can be reduced when the optimal supply air speeds and locations were obtained in pig farms (Tabase et al., Reference Tabase, Bagci, De Paepe, Aarnink and Demeyer2020; Niu et al., Reference Niu, Zhong and Hu2024). At the same time, the energy consumption was proved to be decreased by about 46% for a pig farm with an integrated geothermal heat exchanger (Krommweh et al., Reference Krommweh, Rösmann and Büscher2014). However, ventilation systems in pig farms were limited due to their poor cooling effect during long-term high temperature (Tabase et al., Reference Tabase, Millet, Brusselman, Ampe, Sonck and Demeyer2018; Costantino et al., Reference Costantino, Fabrizio, Villagrá, Estellés and Calvet2020). For the sake of sustainable development and system performance improvement, ground source heat pump systems were used in pig industries (Mun et al., Reference Mun, Dilawar, Rathnayake, Chung, Kim, Ryu, Park, Lee and Yang2021). However, there were some issues that hindered their development, such as expensive initial investment (Mun et al., Reference Mun, Dilawar, Jeong, Rathnayake, Won, Park, Lee, Ryu and Yang2020), climate and geographical limitations (Licharz et al., Reference Licharz, Rösmann, Krommweh, Mostafa and Büscher2020; Blázquez et al., Reference Blázquez, Borge-Diez, Nieto, Maté-González, Martín and González-Aguilera2022). In pig farms with floor cooling systems, the production performance can be improved for sows under heat stress (Riskowski et al., Reference Riskowski, Shaffer and Harrison2017; Parois et al., Reference Parois, Cabezón, Schinckel, Johnson, Stwalley and Marchant-Forde2018). However, local high temperature and high operating costs are the main problems when floor cooling systems were used in pig farms. Currently, evaporative misting systems were the common temperature regulation systems in pig farms due to their considerable economic benefits (Tajudeen et al., Reference Tajudeen, Moturi, Hosseindoust, Ha, Mun, Choi, Sa and Kim2022). Specifically, the appropriate indoor temperature was regulated and energy consumption was significantly reduced in pig farms with evaporative misting systems (Lontoc et al., Reference Lontoc, Punay, Cajano and Vega2018; Wiegert et al., Reference Wiegert, Knauer and Shah2022). However, under high humidity conditions, less heat was absorbed by evaporative cooling and the cooling effect was worse for evaporative misting systems (Haeussermann et al., Reference Haeussermann, Hartung, Jungbluth, Vranken, Aerts and Berckmans2007; Hu et al., Reference Hu, Yang, Tao, Shi, Tu and Wang2023). Therefore, improving the cooling effect under high humidity conditions was an urgent problem to be solved for evaporative misting systems because it had a significant impact on the economic benefits of pig industries. Dehumidification before evaporative misting was considered as one of the effective methods to improve the evaporative cooling efficiency under high humidity conditions. However, the feasibility of this method in pig farms needed to be confirmed through research and the huge energy consumption of equipment based on this method became a key concern.

With the development of solar energy utilization technology, the evaporative misting systems based on photovoltaic/thermal (PV/T) devices have been developed in residential buildings due to their energy-saving advantages (Sultan et al., Reference Sultan, Miyazaki, Mahmood and Khan2018; Ma et al., Reference Ma, Xie, Duan, Song, Ding and Hou2022; Wang et al., Reference Wang, Yang, Chen, Yu, Zhang, Zou and Ren2023). Redelinghuys et al. (Reference Redelinghuys, Tshamala and Hans2023) investigated an adiabatic pre-cooling mechanical draft system for concentrating solar power plants in arid areas. The results indicated that the cooling parasitic power consumption and power operating costs can be decreased by about 5.37 and 14.19% in adiabatic pre-cooling mechanical draft systems, respectively. In another study, the feasibility of a solar-geothermal system used to provide the energy and water was evaluated for a residential building (Baniasadi et al., Reference Baniasadi, Ziaei-Rad, Behvand and Javani2023). It can be found that the energy efficiency was 13.27–17.25% for the proposed system. Therefore, the power consumption of evaporative misting systems can be decreased when PV/T devices were adopted to provide energy to the systems (Zhang et al., Reference Zhang, He, Song, Wang, Liu, Zhao, Gao, Huang, Han and Qi2023). In addition, some scholars concluded that compared to some ventilation systems, the power consumption and carbon dioxide emissions were decreased by 15–31% in some pig farms with solar air heaters (Mun et al., Reference Mun, Ahmed, Islam, Park and Yang2015; Moon et al., Reference Moon, Lee, Kim, Choi, Kim, Ryou and Kim2017; Yu et al., Reference Yu, Shah, Knauer, Boyette and Stikeleather2021). At the same time, when photovoltaic panels were used in a pig farm, the obtained electric energy was proved to provide 35% of the power consumption for a pig farm (Kwak et al., Reference Kwak, Shin, Kang, Mun, Jo, Kim and Huh2021). The above research indicated that the temperature regulation systems combined with PV/T devices may reduce the energy consumption and operating costs of these systems in pig farms. At the same time, the power consumption of temperature regulation systems can be significantly decreased in the pig farms with ventilation heat exchange (Moon et al., Reference Moon, Kim, Nah, Kim and Kim2015; Ma et al., Reference Ma, Liang, Liu, Luo, Hou and Wang2021a, Reference Ma, Liang, Zhang, Luo, Hou and Wang2021b; Xie et al., Reference Xie, Min, Ma, Ding, Wang and Liu2024). Specifically, the power consumption can be decreased by 46% when the combination of ground source heat pump and ventilation heat exchange was used for temperature regulation in pig farms compared with a ventilation system (Alberti et al., Reference Alberti, Antelmi, Angelotti and Formentin2018; Lapertot et al., Reference Lapertot, Cuny, Kadoch and Le Métayer2021). In an economic study, the energy costs were reduced by 19.7% and an economic benefit of 12 028 euros was obtained per year under this system (Deeken et al., Reference Deeken, Lengling, Krommweh and Büscher2023). In conclusion, dehumidification before evaporative misting is one of the effective methods to improve the evaporative cooling efficiency under high humidity conditions, but it can significantly increase system energy consumption. At the same time, PV/T and ventilation heat exchange devices can contribute to reducing the energy consumption of devices such as dehumidification device and spray device in the system. The coupling of an evaporative misting system with a PV/T system combined with a ventilation heat exchange device may improve the regional applicability of cooling system and produce significant benefits for pig farms. However, the feasibility of this system in pig farms in high-humidity areas need to be confirmed through research. At the same time, the regulation and optimization is difficult for this system due to its numerous devices. Therefore, construct the proposed system, develop its control strategy and quantify its performance to promote its application and improve its benefits.

In this paper, a new evaporative misting system based on PV/T and ventilation heat exchange is proposed and its simulation model is constructed in sow farms. Through simulation, the annual operating modes are obtained for the proposed system in Guangzhou. Meanwhile, the optimal regulation variable ranges in the proposed system are determined for mass flow rate of working fluid (MFWF) and misting power by analysing its operating characteristics. The annual performance variables are further quantified and analysed under different load ratios for the proposed system in Guangzhou.

New system construction

In this section, a new evaporative misting system based on PV/T and ventilation heat exchange is proposed in sow farms, as shown in Fig. 1. The number meaning of the new evaporative misting system is listed in Table 1. The proposed system can be divided into three sub-systems and their operating routes can be distinguished by three different colours in Fig. 1. In this section, the operating process of three sub-systems is explained in detail.

Figure 1. New evaporative misting system constructed in this paper.

Table 1. Number meaning in the new evaporative misting system

The function of sub-system 1 is the conversion, transmission and storage of thermal energy in the proposed system. In sub-system 1, thermal energy can be obtained based on PV/T collectors 1. The obtained thermal energy is absorbed by working fluid through the first circulating pump 2 and subsequently transferred to the working fluid in the first heat exchanger 3. To store the heat obtained from PV/T collectors, it can be transferred to the phase-change material (PCM) in the phase-change heat storage tank (PHST) through the second circulating pump 4. When exhaust air is required to be heated in the heating season, the thermal energy stored in PCM can be absorbed by working fluid and used to heat exhaust air through heat exchange in the second heat exchanger 16. Otherwise, in the cooling season, the stored thermal energy can be used to heat supply air through heat exchange in the third heat exchanger 24. If the heat stored in PCM cannot meet the required heat in the proposed system, the auxiliary heater 6 can provide its heat demand to ensure the system operation.

The function of sub-system 2 is the conversion, transmission and storage of electric energy in the proposed system. Based on PV/T collectors 1, solar energy can be converted into electric energy. The obtained electric energy is converted into alternating current through photovoltaic controller 9 and photovoltaic inverter 10. Through the electrical cabinet 12, alternating current is transmitted to two drive motors and other electrical equipment in the proposed system. At the same time, the converted direct current can be charged in the battery 11 through photovoltaic controller 9 when the power demand is met for the proposed system. In addition, the surplus electric energy can be transmitted to the public electricity network for electricity sale through the electrical cabinet 12. If the electric energy consumed by equipment cannot be met by the electric energy obtained from PV/T collectors, the public electricity network can provide the electricity required by the proposed system to ensure the system operation.

The function of sub-system 3 is the heat exchange and temperature regulation of exhaust and supply air in the proposed system. In the route of supply air, if the humidity of supply air exceeds the set humidity, it will be dehumidified by desiccant materials in the desiccant wheel 21 and subsequently sent into the heat exchange device 22 through supply fan 20. In the heat exchange device 22, the heat is recovered through the heat exchange between exhaust and supply air. Then, the air conditioning mode in the proposed system is further obtained based on the set temperature. In the cooling season, if the set temperature is higher than the temperature of supply air, the additional heat of supply air will be eliminated through heat exchange with cooling water in the spray device 23. In the heating season, if the temperature of supply air is higher than the set temperature, the heat of working fluid will be absorbed by supply air in the third heat exchanger 24. When the temperature of supply air meets the requirements, supply air will not be processed and sent into a sow farm. In the route of exhaust air, the ammonia will be absorbed by circulating water added with absorbent in the acid spray scrubber 17. After exhaust air is eliminated from odour, its heat is recovered through heat exchange in the heat exchange device 22. In the cooling season, exhaust air will be further used for the regeneration of desiccant materials when the supply air does not meet the requirement. Specifically, the heat of exhaust air is obtained by exchanging heat with working fluid in the second heat exchanger 16. The heated exhaust air can absorb moisture from desiccant materials in the desiccant wheel 21 to achieve the recycling of desiccant materials. Finally, exhaust air is sent outdoors through exhaust fan 15.

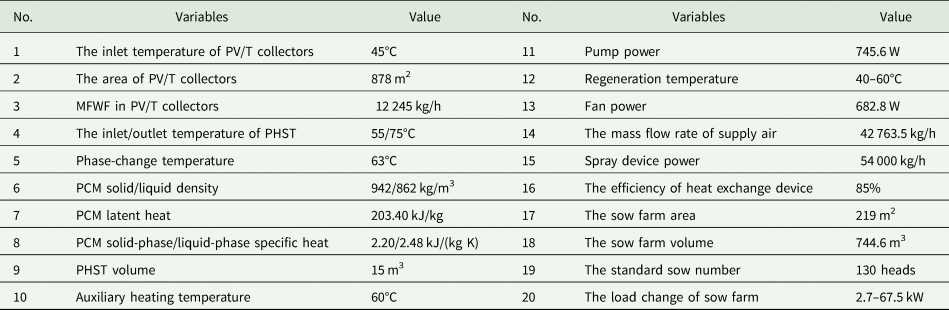
The main design and operating variables are shown in Table 2 for the applied sow farm and the proposed system. It can be concluded that compared to the existing evaporative misting systems, the proposed system can help to improve its efficiency of evaporative cooling under high humidity conditions due to solar dehumidification and reduce the energy consumption of existing systems due to solar energy benefits (SEB) and ventilation heat exchange. In other words, the proposed system can improve the regional applicability of existing evaporative misting systems, and reduce their energy consumption and carbon emissions in sow farms.

Table 2. Main design and operating variables of the applied sow farm and the proposed system

Models of core equipment

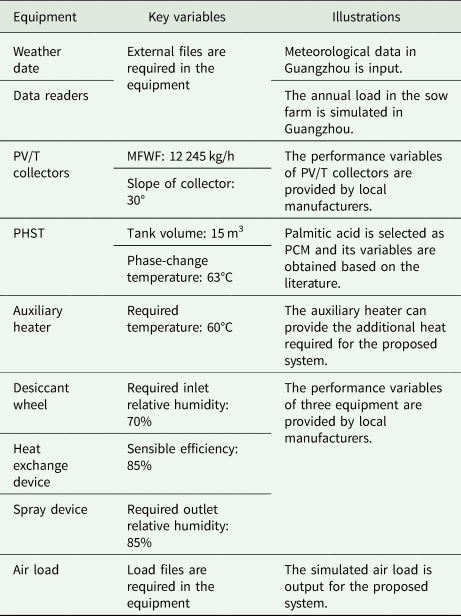
Based on the new evaporative misting system, the core equipment of the proposed system includes desiccant wheel, PV/T collectors and PHST. To ensure the accuracy of system simulation, the core equipment of the proposed system, including desiccant wheel, PV/T collectors and PHST, is newly built based on the equipment library of TRNSYS software (TESS Library Documentation, 2006; Ma et al., Reference Ma, Xie, Min, Chen, Liu, Wang, Ding and Cai2023e). For the detailed modelling process, refer to Appendixes A–C. The meaning of variable symbols can be obtained in Nomenclature.

New system model

To simulate the annual operation of the proposed system, its simulation model is constructed based on TRNSYS software, as shown in Fig. 2. Some equipment and its variables in the proposed system simulation model are shown in Table 3. The operating routes of three working media can be distinguished by three different colours in the proposed system simulation model. In this section, their operating process is explained in detail.

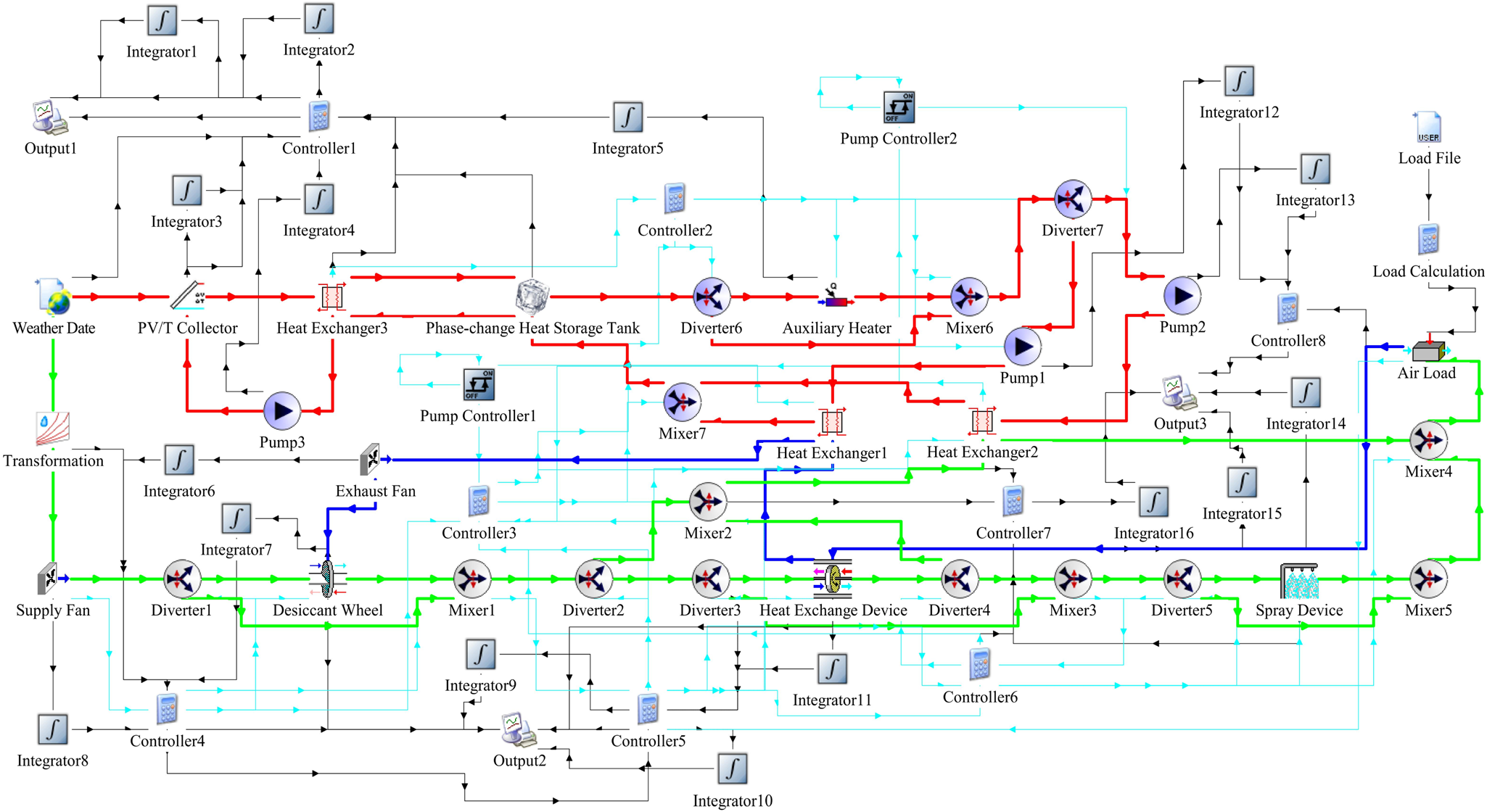
Figure 2. Proposed system simulation model based on TRNSYS software.

Table 3. Some equipment and its variables in the proposed system simulation model

In the proposed system simulation model, the operating routes of supply air are shown by the green line. At first, the outdoor air temperature and humidity can be input from meteorological data in Guangzhou. Through diverter 1, the flow route of supply air is obtained based on the required relative humidity. If the humidity of supply air exceeds the set humidity, supply air will be sent into mixer 1 after being dehumidified by desiccant materials. On the contrary, it will not be processed and sent into mixer 1. Then, the flow route of supply air is obtained based on the set temperature through diverters 2 and 3. If the temperature of exhaust air is higher than that of supply air in the cooling season, it will not be processed and sent into mixer 3. On the contrary, supply air will be sent to diverter 4 after being cooled in the heat exchange device. If the temperature of supply air exceeds that of exhaust air in the heating season, it will not be processed and sent into mixer 3. On the contrary, supply air will be sent into diverter 4 after being heated in the heat exchange device. If the temperature of supply air from the heat exchange device is still lower than the set temperature, it will be heated to the set temperature in the heat exchanger 2. On the contrary, it will not be processed and sent into mixer 3. Through diverter 5, the flow route of supply air is further obtained based on the set temperature. If the temperature of supply air is lower than the set temperature, it will not be processed and sent into mixer 5. On the contrary, supply air will be sent into mixer 5 after being cooled in a spray device. The temperature and humidity of supply air gathered in mixer 4 will be changed based on the simulated air load in the sow farm.

According to the proposed system simulation model, the operating routes of exhaust air are shown by the blue line. At first, the exhaust air temperature and humidity can be input from the air load equipment. Then, exhaust air will be sent into the heat exchanger 1 after being cooled or heated in the heat exchange device. If the humidity of supply air exceeds the set humidity, exhaust air will be heated in the heat exchanger 1. The heated exhaust air is used for the regeneration of desiccant materials in the desiccant wheel. On the contrary, it will not be processed and sent outdoors through exhaust fans.

In the proposed system simulation model, the operating routes of working fluid are shown by the red line. The annual electricity converted from solar energy is recorded through output 1. At the same time, the heat converted from solar energy is absorbed by working fluid in PV/T collectors for the heat supply air. The heat absorbed by working fluid is transferred to PCM in PHST through heat exchange in the heat exchanger 3. If there is a heat demand in the proposed system, the working fluid is sent into diverter 6 after absorbing the heat from PCM. Through diverter 6, the flow route of working fluid is obtained based on the set temperature. If the temperature of working fluid exceeds the set temperature, it will not be processed and sent into mixer 6. On the contrary, working fluid will be sent into mixer 6 after being heated by auxiliary heater. Then, the flow route of working fluid is obtained based on the set temperature through diverter 7. If supply air needs to be heated, the heat of working fluid will be absorbed by supply air through heat exchange in the heat exchanger 2. On the contrary, the heat of working fluid will be absorbed by exhaust air through heat exchange in the heat exchanger 1. After the thermal energy of working fluid is absorbed by exhaust air or supply air, it will be sent into PHST for circulation.

Model validation and performance evaluation

Model validation of core equipment

In this section, the core equipment models in the proposed system are validated to ensure the accuracy of system simulation. Based on the cited literature, the conditions adopted for verification are listed in Table 4. The same design and operating conditions as in the literature (Jia et al., Reference Jia, Dai, Wu and Wang2006) are adopted to validate the model of desiccant wheel. Specifically, the simulated dehumidification capacity is compared with the experimental dehumidification capacity in the literature (Jia et al., Reference Jia, Dai, Wu and Wang2006) under different inlet temperature conditions of desiccant wheel. Figure 3 shows the errors between the experimental dehumidification capacity and simulated data in the range of 18–40°C at the inlet of desiccant wheel. It can be found that the maximum error between the experimental dehumidification capacity and simulated data is 6.8%. At the same time, the same design and operating conditions as in the literature (Mahmoud et al., Reference Mahmoud, Houcine, Guizani and Maalej2005) are adopted to validate the PV/T collector model. Specifically, the simulated outlet temperature is compared with the experimental outlet temperature in the literature (Mahmoud et al., Reference Mahmoud, Houcine, Guizani and Maalej2005) under different inlet temperature conditions of PV/T collectors. Figure 4 shows the errors between the experimental and simulated outlet temperature in the range of 28–40°C at the inlet of PV/T collectors. It can be found that the maximum error between the experimental and simulated outlet temperatures is 6.78%. When the same design and operating conditions as in the literature (Ibanez et al., Reference Ibanez, Cabeza, Solé, Roca and Nogués2006) are adopted to validate the model of PHST, PCM heated to 70°C exchanges heat with cooling water and the change of middle temperature is tested in PHST within 30 min. The change of simulated middle temperature is compared with that of experimental middle temperature in the literature (Ibanez et al., Reference Ibanez, Cabeza, Solé, Roca and Nogués2006) in 30 min after the heat exchange between PCM and circulating water. Figure 5 shows the errors between experimental and simulated middle temperatures within 30 min after the heat exchange between PCM and circulating water. It can be found that the maximum error between the experimental and simulated middle temperatures is 14.5%. In summary, it can be concluded that the models of core equipment can meet the simulation accuracy.

Table 4. Conditions adopted for verification based on the cited literature

Figure 3. Errors between the experimental dehumidification capacity and simulated data in the range of 18–40°C at the inlet of desiccant wheel.

Figure 4. Errors between the experimental and simulated outlet temperatures in the range of 28–40°C at the inlet of PV/T collectors.

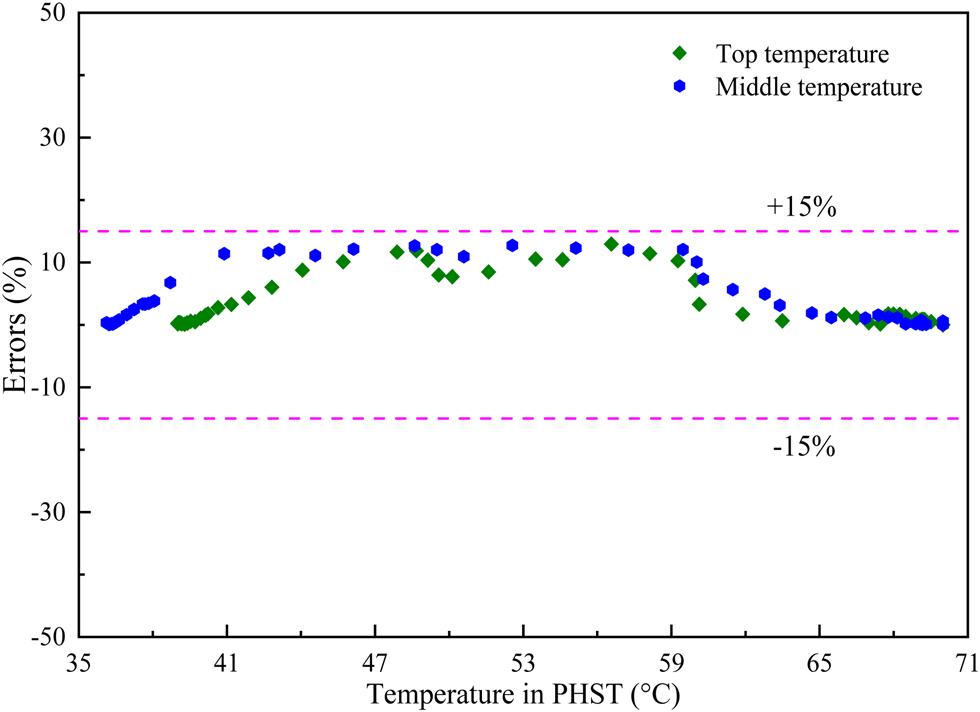
Figure 5. Errors between experimental and simulated middle temperatures within 30 min after the heat exchange between PCM and circulating water.

Performance evaluation variables

To quantify the proposed system performance, some performance evaluation variables are used in this paper. These variables include the exergy loss, energy consumption, heat exchange coefficient (HEC), energy efficiency ratio (EER) and SEB of the proposed system. Their calculation is described in this section.

Exergy loss

In the proposed system, exergy loss is used to reflect the changes of energy quality. It can be obtained by the following equation:

(1)$$E_{{\rm loss}} = \Delta E_{{\rm in}}-\Delta E_{{\rm out}}$$

where E loss is the exergy loss of the proposed system, kW; ΔE in is the input exergy of the proposed system, kW and ΔE out is the out exergy loss of the proposed system, kW. The exergy composition and calculation of the proposed system can be found in the literature (Ma et al., Reference Ma, Xie, Min, Liu, Wang, Ding and Luo2023f).

Heat exchange coefficient

It can be found that the electric energy is consumed and the air heat is recovered in the heat exchange device. In this paper, HEC is used to evaluate the heat exchange benefits of the proposed system. It can be obtained by the following equation:

(2)$$HEC = \displaystyle{{Q_{\rm f}} \over {P_{\rm r}}} = \displaystyle{{m_{\sup }( {h_{{\rm sup, out}}-h_{{\rm sup, in}}} ) } \over {P_{\rm r}}}$$

where Q f is the heat exchange between exhaust and supply air, kJ; P r is the electric energy consumed by heat exchange device, kJ; m sup is the mass flow rate of supply air, kg/s and h sup,in and h sup,out are the unit enthalpy of supply air at the inlet and outlet of heat exchange devices, respectively.

Energy efficiency ratio

To evaluate the heating and cooling device efficiency, EER is considered as one of the important performance evaluation variables. It can be obtained by the following equation:

(3)$$EER_{\rm h} = \displaystyle{{\sum {{\dot{Q}}_{\rm h}} } \over {\sum {{\dot{P}}_{\rm h}} }} = \displaystyle{{Q_{\rm h}} \over {P_{\rm h}}}$$
(4)$$EER_{\rm c} = \displaystyle{{\sum {{\dot{Q}}_{\rm c}} } \over {\sum {{\dot{P}}_{\rm c}} }} = \displaystyle{{Q_{\rm c}} \over {P_{\rm c}}}$$

where $\dot{Q}_{\rm c}$ and $\dot{Q}_{\rm h}$ are the cooling and heating capacity of the proposed system per unit time, respectively, kW; $\dot{P}_{\rm c}$ and $\dot{P}_{\rm h}$ are the power consumption of cooling and heating equipment per unit time, respectively, kW; Q c and Q h are the heat of wet air obtained in heating and cooling equipment, respectively, kJ and P c and P h are the electric energy consumed by heating and cooling equipment, respectively, kJ.

Results

The main purpose of this paper is to determine the feasibility and application benefits of the proposed system in high-humidity areas. In this paper, as a typical high-temperature and high-humidity area, Guangzhou is considered as the application area for the proposed system. Specifically, the annual operating modes and optimal regulation variable ranges are determined for the proposed system in Guangzhou through simulation. Further, the regulation suggestions will be obtained for the proposed system when it is operated under high-temperature and high-humidity conditions.

Annual operating modes and optimal regulation variable ranges

Annual operating modes

Before analysing the annual performance of the proposed system in Guangzhou, it is crucial to determine its annual operating modes and optimal regulation variable ranges through simulation. Based on the outdoor climate characteristics in Guangzhou, the annual operating modes are obtained for the proposed system to ensure the maximum utilization of heating and cooling devices. Figure 6 shows the annual outdoor temperature changes in Guangzhou and indoor temperature changes under the regulation of the proposed system. It can be found that outdoor temperature in Guangzhou and indoor temperature regulated by the proposed system are in the range of 4–39 and 18–27°C throughout the year, respectively. This indicates that the indoor temperature regulated by the proposed system can meet the set temperature range of 18–27°C in sow farms (Santonja et al., Reference Santonja, Georgitzikis, Scalet, Montobbio, Roudier and Sancho2017). To ensure the feasibility of solar energy utilization technology in the proposed system, the solar radiation in Guangzhou and the solar fraction of the proposed system are analysed for a whole year in this section, as shown in Fig. 7. The results show that in Guangzhou, the abundant annual solar radiation provides a foundation for the solar energy utilization in the proposed system. Specifically, when the solar radiation is higher than 193.7 W/m2, it can be found that the required heat in the proposed system can be provided by PV/T collectors through simulation. At the same time, it can be found that in the proposed system, the achieved monthly solar fraction ranges from 38.17 to 48.23%. In other words, in Guangzhou, the required heat in the proposed system can be partially obtained from PV/T collectors, but the required additional heat can be provided by auxiliary heater. Aiming at the optimization of system performance in Guangzhou, the annual operating modes of the proposed system are obtained based on its simulation model. Figure 8 shows the energy consumption of heating and cooling devices in the proposed system for a whole year. To improve the utilization efficiency of heating and cooling devices, the annual operating modes can be obtained for the proposed system. It can be found that the annual operating modes of the proposed system in Guangzhou can be divided into heating and cooling seasons. Specifically, in the sow farm, the heating season is from 1st January to 5th March and 31st October to 31st December, and the cooling season is from 5th March to 31st October. According to the annual operating modes of the proposed system in Guangzhou, its annual operating characteristics are analysed to obtain its annual optimal regulation variable ranges through simulation.

Figure 6. Annual outdoor temperature changes in Guangzhou and indoor temperature changes under the regulation of the proposed system.

Figure 7. Solar radiation in Guangzhou and the solar fraction of the proposed system in the whole year.

Figure 8. Energy consumption of heating and cooling devices in the proposed system for a whole year.

Optimal regulation variable ranges

Based on the above results, the annual operating characteristics are analysed and the optimal regulation variable ranges are further obtained for the proposed system in Guangzhou. For the sake of the temperature requirements of sow house, the heating and cooling powers of the proposed system in Guangzhou are regulated by changing its MFWF and misting power. Figure 9 shows the indoor time percentage at 18–27°C in the cooling season under different misting powers when MFWF is 7245 kg/h for the proposed system in Guangzhou. It can be found that when the misting power of the proposed system increases from 25 to 40 kW, the indoor time percentage at 18–27°C in the cooling season increases from 61.9 to 100%. However, it remains at 100% when the misting power of the proposed system increases from 40 to 45 kW. In other words, when the misting power of the proposed system is 25–40 kW, the indoor time percentage at 18–27°C in the cooling season is positively correlated with misting power. At the same time, the indoor time percentage at 18–27°C can be maintained at 100% in the cooling season when the misting power of the proposed system is 40–45 kW. Figure 10 shows the indoor time percentage at 18–27°C in the heating season under different MFWFs when the misting power is 40 kW for the proposed system in Guangzhou. The results show that when the MFWF of the proposed system increases from 7245 to 9245 kg/h, the indoor time percentage at 18–27°C in the heating season remains at 100%. However, it decreases from 100 to 75.8% when the MFWF of the proposed system increases from 9245 to 155 245 kg/h. In other words, when the MFWF of the proposed system is 9245–155 245 kg/h, the indoor time percentage at 18–27°C in the heating season is negatively correlated with MFWF. At the same time, the indoor time percentage at 18–27°C can be maintained at 100% in the heating season when the MFWF of the proposed system is 7245–9245 kg/h. To sum up, the optimal ranges of MFWF and misting power are 7245–9245 kg/h and 40–45 kW for the proposed system in Guangzhou, respectively.

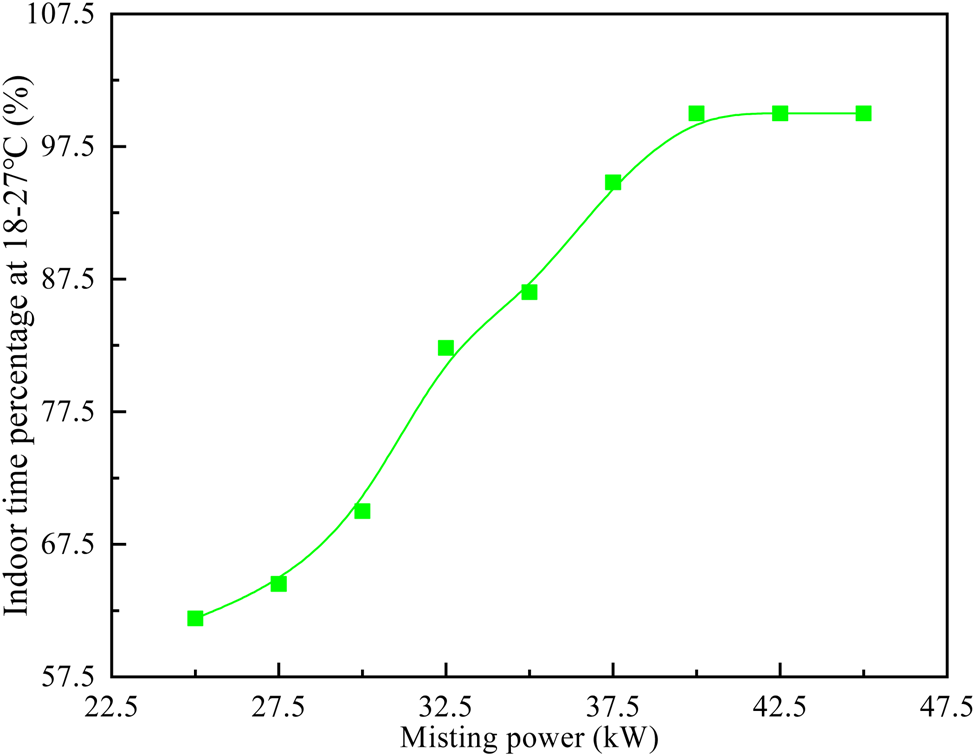
Figure 9. Indoor time percentage at 18–27°C in the cooling season under different misting powers when MFWF is 7245 kg/h for the proposed system in Guangzhou.

Figure 10. Indoor time percentage at 18–27°C in the heating season under different MFWFs when the misting power is 40 kW for the proposed system in Guangzhou.

System performance analysis

Energy consumption and exergy loss

To determine its performance advantages in Guangzhou and guide its operating regulation, the annual energy consumption and exergy loss are further analysed for the proposed system through simulation based on its annual operating modes and optimal regulation variable ranges. At the same time, according to the simulation results, it can be found that the indoor load has a significant influence on the proposed system performance. In other words, the performance changes of the proposed system are significantly related to the indoor sow density. Therefore, the annual exergy loss and energy consumption of the proposed system in Guangzhou are analysed under different load ratios (sow densities) through simulation. Figures 11 and 12 show the annual energy consumption and exergy loss of the proposed system in Guangzhou under different load ratios, respectively. It can be found that in the cooling season, when load ratio changes from 30 to 140%, the exergy loss of the proposed system decreases from 9.62 × 104 to 9.07 × 104 kW. However, in this case, its energy consumption increases from 1.48 × 105 to 1.57 × 105 kJ. In other words, in the cooling season, the exergy loss of the proposed system decreases with the increase of load ratio, but its energy consumption increases with the increase of that. Similarly, in the heating season, when load ratio changes from 30 to 140%, the exergy loss of the proposed system decreases from 6.52 × 104 to 6.18 × 104 kW. However, in this case, its energy consumption increases from 4.73 × 105 to 4.94 × 105 kJ. In other words, in the heating season, the exergy loss of the proposed system decreases with the increase of load ratio, but its energy consumption increases with the increase of load ratio. Through analysis, the above changes are because there are differences in the annual SEB, heat exchange efficiency and EER of the proposed system. In addition, it can be found that when load ratio changes from 30 to 120%, the annual exergy loss changes significantly, but it changes slightly when load ratio exceeds 120% in sow farms. This indicates that the exergy loss of the proposed system is significantly affected by load ratio when load ratio does not exceed 120% (the indoor sow density does not exceed 0.7 heads/m2 in sow farms). At the same time, the system performance and benefits are not significantly improved by increasing device investment and sow density when load ratio exceeds 120% in sow farms. In summary, the annual exergy loss of the proposed system in Guangzhou decreases with the increase of load ratio, but its energy consumption increases with the increase of load ratio. These changes are because there are differences in the annual SEB, heat exchange efficiency and EER of the proposed system. At the same time, the system performance and benefits are not significantly improved by increasing device investment and sow density when load ratio exceeds 120% in sow farms.

Figure 11. Energy consumption and exergy loss of the proposed system in Guangzhou under different load ratios in the cooling season.

Figure 12. Energy consumption and exergy loss of the proposed system in Guangzhou under different load ratios in the heating season.

HEC and EER

According to the above analysis, the differences in annual exergy loss and energy consumption of the proposed system are because there are differences in its annual SEB, heat exchange efficiency and EER. In this section, the annual HEC and EER of the proposed system in Guangzhou are analysed under different load ratios through simulation to determine its energy efficiency and heat exchange efficiency. Figures 13 and 14 show the annual HEC and EER of the proposed system in Guangzhou under different load ratios, respectively. It can be found that in the cooling season, when load ratio changes from 30 to 140%, the HEC of the proposed system decreases from 89.58 to 85.54%. However, in this case, its EERc increases from 4.28 to 4.53. In other words, in the cooling season, the HEC of the proposed system is negatively correlated with load ratio, but its EERc increases with the increase of load ratio. Similarly, in the heating season, when load ratio changes from 30 to 140%, the HEC of the proposed system decreases from 132.01 to 109.71. However, in this case, its EERh increases from 4.11 to 4.33. In other words, in the heating season, the HEC of the proposed system is negatively correlated with load ratio, but its EERh increases with the increase of load ratio. However, it can be found that the HEC of the proposed system is less affected by load ratio than its EER. Through analysis, the above changes are because the increase in sow number leads to a significant increase in the heating and cooling capacity of the proposed system, but a decrease in the heat exchange between exhaust and supply air. In addition, it can be found that when load ratio changes from 30 to 120%, the annual HEC and EER change significantly, but they change slightly when load ratio exceeds 120% in sow farms. This shows that the energy efficiency and heat exchange efficiency of the proposed system is significantly affected by load ratio when load ratio does not exceed 120% (the indoor sow density does not exceed 0.7 heads/m2 in sow farms). At the same time, the system performance and benefits are not significantly improved by increasing device investment and sow density when load ratio exceeds 120% in sow farms. In summary, the annual HEC of the proposed system in Guangzhou is negatively correlated with load ratio, but its annual EER increases with the increase of load ratio. However, the HEC of the proposed system is less affected by load ratio than its EER. These changes are because the increase in sow number leads to a significant increase in the heating and cooling capacity of the proposed system, but a decrease in the heat exchange between exhaust and supply air. At the same time, the system performance and benefits are not significantly improved by increasing device investment and sow density when load ratio exceeds 120% in sow farms.

Figure 13. HEC and EER of the proposed system in Guangzhou under different load ratios in the cooling season.

Figure 14. HEC and EER of the proposed system in Guangzhou under different load ratios in the heating season.

Solar energy benefits

To determine its SEB, the annual SEB of the proposed system are further obtained under different load ratios. The annual SEB of the proposed system in Guangzhou under different load ratios is shown in Fig. 15. It can be found that when load ratio changes from 30 to 140%, the annual SEB of the proposed system decreases from 4.72 × 105 and 2.39 × 105 kJ to 2.66 × 105 and 2.07 × 105 kJ, respectively. Through analysis, the above changes are because the increase in sow number leads to a significant increase in the heating and cooling capacity of the proposed system, but a decrease in the usable heat obtained by the proposed system. In summary, the annual SEB of the proposed system in Guangzhou are negatively correlated with load ratio. These changes are because the increase in sow number leads to a significant increase in the heating and cooling capacity of the proposed system, but a decrease in the usable heat obtained by the proposed system.

Figure 15. Annual SEB of the proposed system in Guangzhou under different load ratios.

Conclusion

A new evaporative misting system based on PV/T and ventilation heat exchange was proposed in sow farms in this paper. Further, the simulation model was constructed for the above system. Through simulation, the annual operating modes were obtained for the proposed system in Guangzhou. Meanwhile, the optimal regulation variable ranges were determined for MFWF and misting power in the proposed system. The annual performance variables, including exergy loss, energy consumption, HEC, EER and SEB, were quantified and analysed under different load ratios for the proposed system in Guangzhou. The main conclusions can be obtained as follows:

  1. (1) Through the improvement of existing spray cooling system, the annual indoor temperature can be maintained between 18 and 27°C and the monthly solar fraction can be maintained between 38.17 and 48.23% in the proposed system in high-temperature and high-humidity areas.

  2. (2) The annual operating modes of the proposed system in Guangzhou mainly include heating and cooling seasons. Specifically, in the sow farm, the heating season is from 1st January to 5th March and 31st October to 31st December, and the cooling season is from 5th March to 31st October. Meanwhile, the optimal ranges of MFWF and misting power are 7245–9245 kg/h and 40–45 kW for the proposed system in Guangzhou, respectively.

  3. (3) The annual exergy loss, HEC and SEB of the proposed system in Guangzhou are negatively correlated with load ratio, but its annual energy consumption and EER are positively correlated with that. At the same time, the HEC of the proposed system is less affected by load ratio than its EER. These changes are because the increase in sow number leads to a significant increase in the heating and cooling capacity of the proposed system, but a decrease in the usable heat obtained by the proposed system and the heat exchange between exhaust and supply air.

  4. (4) The exergy loss, HEC and EER of the proposed system is significantly affected by load ratio when load ratio does not exceed 120% in sow farms. Meanwhile, the system performance and benefits are not significantly improved by increasing device investment and sow density when load ratio exceeds 120% in sow farms.

Author contributions

Yue Xie: conceptualization, investigation, methodology, writing – original draft, formal analysis, supervision and project administration. Qinghua Li: software, validation and investigation. Hongqiang Ma: writing – review and editing, supervision. Jiajun Wang: writing – review and editing, supervision. Shengxun Wang: writing – review and editing, supervision.

Funding statement

The authors are grateful for the support from the National Natural Science Foundation of China (52368071) and Jiangxi Province Innovation Leading Talent Project (jxsq2023101064 and jxsq2023102132).

Competing interests

None.

Nomenclature

a half height of air channels, m

A cross-sectional area of air channels, m2

A bottom surface area at the bottom of PHST, m2

A edges surface area at the edges of PHST, m2

A top surface area at the top of PHST, m2

A ut surface area of adsorbent in the wheel per unit volume, m2/m3

b half width of air channels, m

B r proportion of the airflow area to the total cross-sectional area of wheel on the airflow section

c a specific heat capacity of air, kJ/(kg K)

c mat specific heat capacity of matrix material, kJ/(kg K)

c mean mean specific heat capacity of fluid in PHST, kJ/(kg K)

c pcm specific heat capacity of PCM in the actual heat transfer process, kJ/(kg K)

c pf specific heat capacity of supply air, kJ/(kg K)

c p,fluid specific heat capacity of fluid in PHST, kJ/(kg K)

c p,hx specific heat capacity of fluid in the immersed heat exchanger, kJ/(kg K)

c s specific heat capacity of desiccant material, kJ/(kg K)

c u specific heat capacity of water vapour, kJ/(kg K)

c w specific heat capacity of water, kJ/(kg K)

d ad moisture content of air at the surface of adsorbent, g/kg

d exh,in moisture content of exhaust air at the inlet of desiccant wheel, g/kg

d m moisture content of desiccant material, g/kg

d pro dehumidification capacity of process air, g/kg

d pro,in moisture content of process air at the inlet of desiccant wheel, g/kg

d rec moisture content of exhaust air, g/kg

d sup moisture content of supply air, g/kg

D v diffusion coefficient of water vapour, m2/s

E loss exergy loss of the proposed system, kW

f mat mass of matrix material per unit length, kg

f sg mass of desiccant material per unit length, kg

h y convection heat transfer coefficient between air and desiccant material, W/(m2 K)

h ad convection heat transfer coefficient between air and adsorbent, W/(m2 K)

h sup,in enthalpy of supply air at the inlet of heat exchange device, J/kg

h sup,out enthalpy of supply air at the outlet of heat exchange device, J/kg

k a air thermal conductivity, W/(m K)

k s thermal conductivity of PCM, W/(m K)

K ad mass transfer coefficient between air and adsorbent, kg/(m2 s)

K y mass transfer coefficient between air and desiccant material, kg/(m2 s)

L a perimeter of air channels, m

m exh mass flow rate of exhaust air, kg/s

m hx,in mass flow rate of fluid flowing into the immersed heat exchanger, kg/h

m sup mass flow rate of supply air, kg/s

m tank,in mass flow rate of fluid flowing into PHST, kg/h

m ua mass flow rate of air per unit cross-sectional area of wheel, kg/(m2 s)

Nu Nusselt number

p a air pressure, kPa

p r wheel pressure, kPa

p ws saturated water vapour pressure, kPa

P c electric energy consumed cooling equipment, kJ

P h electric energy consumed heating equipment, kJ

P r electric energy consumed by heat exchange device, kJ

$\mathop {P_{\rm c}}\limits^\cdot$ power consumption of cooling equipment per unit time, kW

$\mathop {P_{\rm h}}\limits^\cdot$ power consumption of heating equipment per unit time, kW

q solar irradiance received by PV/T collector, W/m2

q s relative amount of water in desiccant material, kg/kg

Q c heat of wet air obtained in cooling equipment, kJ

Q exh heat obtained by exhaust air in desiccant wheel, W

Q f heat exchange between exhaust and supply air, kJ

Q flow heat transfer rate of fluid flowing into PHST, kJ/h

Q h heat of wet air obtained in heating equipment, kJ

Q hx heat transfer rate of fluid flowing into the immersed heat exchanger, kJ/h

Q in,tank heat transfer rate of fluid at the inlet of PHST, kJ/h

Q loss,bottom heat transfer rate between PHST and the ambient temperature at the bottom of PHST, kJ/h

Q loss,edges heat transfer rate between PHST and the ambient temperature at the edges of PHST, kJ/h

Q loss,top heat transfer rate between PHST and the ambient temperature at the top of PHST, kJ/h

Q out,tank heat transfer rate of fluid at the outlet of PHST, kJ/h

Q pro heat obtained by process air in desiccant wheel, W

$\dot{Q}_{\rm c}$ cooling capacity of systems per unit time, kW

$\dot{Q}_{\rm h}$ heating capacity of systems per unit time, kW

r distance from the central axis of PHST, m

${\mathop{\rm Re}\nolimits}$ Reynolds number

RH s relative humidity of desiccant material, %

Sh Sherwood number

t time, s

t ab temperature of photovoltaic panel, °C

t abs desiccant material temperature, K

t ad adsorbent temperature, K

t c,in air temperature at the inlet of cooling equipment, °C

t c,out air temperature at the outlet of cooling equipment, °C

t env,bottom ambient temperature at the bottom of PHST, °C

t env,edges ambient temperature at the edges of PHST, °C

t env,top ambient temperature at the top of PHST, °C

t h,in air temperature at the inlet of heating equipment, °C

t h,out air temperature at the outlet of heating equipment, °C

t in,hx temperature of fluid flowing into the immersed heat exchanger, °C

t in,tank temperature of fluid flowing into PHST, °C

t o ambient temperature, K

t out,hx temperature of fluid flowing out of the immersed heat exchanger, °C

t pcm PCM temperature in the actual phase-change process, K

t s solar radiation temperature, K

t tank mean temperature of PHST, °C

t w,in inlet temperature of PV/T collector, °C

t w,out outlet temperature of PV/T collector, °C

u air flow velocity, m/s

U bottom heat loss coefficient at the bottom of PHST

U edges heat loss coefficient at the edges of PHST

U top heat loss coefficient at the top of PHST

ν y vertical velocity of PCM under gravity, m/s

W humidity ratio of wet air, g/kg

W s humidity ratio of desiccant material, g/kg

W y humidity ratio of isothermal wet air containing desiccant material, g/kg

Greek letters

ΔE in input exergy of systems, kW

ΔE out output exergy of systems, kW

ΔE s solar radiation, kJ

ΔH a latent heat of water evaporation, kJ/kg

ΔH pcm latent heat in the actual phase-change process, kJ/kg

ΔH u adsorption heat of desiccant material, kJ/kg

η hx heat transfer efficiency of immersed heat exchanger, %

ρ a air density, kg/m3

ρ s PCM Density, kg/m3

ω angular velocity of wheel, rad/s

Appendix A

In this paper, the model of desiccant wheel is built based on some assumptions (Ma et al., Reference Ma, Xie, Li, Zhang, Liu and Luo2023a, Reference Ma, Xie, Wang, Min, Luo and Cai2023b, Reference Ma, Xie, Wang, Liu and Ding2023c, Reference Ma, Xie, Song, Liu, Luo and Wang2023d, Reference Ma, Xie, Min, Chen, Liu, Wang, Ding and Cai2023e, Reference Ma, Xie, Min, Liu, Wang, Ding and Luo2023f). The simplified modelling process of desiccant wheel is as follows:

The perimeter L a and cross-sectional area A of air channels can be obtained by the following equation:

(A1)$$L_{\rm a}\approx 2b{\rm} + 2\sqrt {b^2{\rm} + {( {a\pi } ) }^2} \left[{\displaystyle{{3 + {( {{{2b} / {a\pi }}} ) }^2} \over {4 + {( {{{2b} / {a\pi }}} ) }^2}}} \right]$$

The mass balance between desiccant wall and air can be obtained as follows:

(A2)$$\displaystyle{{\partial W} \over {\partial t}} + u\displaystyle{{\partial W} \over {\partial z}} + \theta _1\displaystyle{{\partial D_{\rm m}} \over {\partial t}} = 0$$
(A3)$$\theta _1 = \displaystyle{{\,f_{{\rm sg}}} \over {2A\rho _{\rm a}}}$$

The mass transfer equation of desiccant materials can be obtained by the following equations:

(A4)$$\displaystyle{{\partial D_{\rm m}} \over {\partial t}} + \theta _2( {W_{\rm y}-W} ) = 0$$
(A5)$$\theta _2 = \displaystyle{{2K_{\rm y}p_{\rm r}} \over {\,f_{{\rm sg}}}}$$

The energy balance between air and desiccant wall can be obtained by the following equations:

(A6)$$\displaystyle{{\partial T} \over {\partial t}} + u\displaystyle{{\partial T} \over {\partial z}} + \theta _3\displaystyle{{\partial T_{{\rm abs}}} \over {\partial t}} = \theta _4( {W-W_{\rm y}} ) $$
(A7)$$\theta _3 = \displaystyle{{\,f_{{\rm sg}}( {c_{\rm s} + D_{\rm m}c_{\rm w}} ) + f_{{\rm mat}}c_{{\rm mat}}} \over {2A\rho _{\rm a}( {c_{\rm a} + Wc_{\rm u}} ) }}$$
(A8)$$\theta _4 = \displaystyle{{K_{\rm y}p_{\rm r}\Delta H_{\rm a}} \over {A\rho _{\rm a}( {c_{\rm a} + D_{\rm m}c_{\rm u}} ) }}$$

The heat transfer equation of desiccant wall can be obtained as follows:

(A9)$$\eqalign{& \displaystyle{{\partial T_{{\rm abs}}} \over {\partial t}} + \theta _5( {T_{{\rm abs}}-T} ) + \theta _6( {W_{\rm y}-D_{\rm m}} ) {\rm} + \theta _7( {W_{\rm y}-D_{\rm m}} ) ( {T-T_{{\rm abs}}} ) \cr & = 0}$$
(A10)$$\theta _5 = \displaystyle{{2h_{\rm w}L_{\rm a}} \over {\,f_{{\rm sg}}( {c_{\rm s} + D_{\rm m}c_{\rm w}} ) + f_{{\rm mat}}c_{{\rm mat}}}}$$
(A11)$$\theta _6 = \displaystyle{{2K_{\rm y}\Delta H_{\rm a}} \over {\,f_{{\rm sg}}( {c_{\rm s} + D_{\rm m}c_{\rm w}} ) + f_{{\rm mat}}c_{{\rm mat}}}}$$
(A12)$$\theta _7 = \displaystyle{{2K_{\rm y}p_{\rm r}c_{\rm u}} \over {\,f_{{\rm sg}}( {c_{\rm s} + D_{\rm m}c_{\rm w}} ) + f_{{\rm mat}}c_{{\rm mat}}}}$$
(A13)$$h_{\rm w} = \displaystyle{{NuK_{\rm a}L_{\rm a}} \over {4A}}$$
(A14)$$K_{\rm y}{\rm} = \rho _{\rm a}\displaystyle{{ShD_{\rm v}L_{\rm a}} \over {4A}}$$
(A15)$$D_{\rm v} = \displaystyle{{2.256} \over {\,p_{\rm a}}}\left({\displaystyle{{t_{\rm a} + 273.13} \over {256}}} \right)^{1.81}$$

The adsorption heat of desiccant materials can be obtained by the following equation:

(A16)$$Q = \Delta H_{\rm u}( {1 + 0.2843{\rm e}^{{-}10.28q_{\rm s}}} ) $$

The correlation between humidity and relative humidity can be obtained by the following equation:

(A17)$$D_{\rm r}{\rm} = \displaystyle{{0.62188RH_{\rm s}} \over {{{\,p_{\rm a}} / {\,p_{{\rm ws}}}}-RH_{\rm s}}}$$

Appendix B

In this paper, the model of PV/T collectors is built to ensure the simulation accuracy. The energy conduction is ignored along the surface of photovoltaic panel and the energy balance equation at any point on the surface of that can be obtained by the following equation:

(B1)$$J-h_{{\rm pe}}( {t_{{\rm ph}}-t_{{\rm en}}} ) -\alpha _{{\rm ra}}( {t_{{\rm ph}}-t_{{\rm sky}}} ) -\displaystyle{{t_{{\rm ph}}-t_{{\rm ab}}} \over R} = 0$$

Among them, h ra and J can be obtained as follows:

(B2)$$h_{{\rm ra}} = \varepsilon \sigma ( {t_{{\rm ph}} + t_{{\rm sky}}} ) ( {t_{{\rm ph}}^2 + t_{{\rm sky}}^2 } ) $$
(B3)$$J = I_{\rm n}\alpha _{{\rm im}}G_{\rm s}( {1-\eta_{{\rm ph}}} ) $$

Among them, η ph is photovoltaic efficiency and obtained by the following equations:

(B4)$$\eta _{{\rm ph}}{\rm} = \eta _{{\rm stc}}\beta _{{\rm temp}}\beta _{{\rm rad}}$$
(B5)$$\beta _{{\rm temp}}{\rm} = 1 + \eta _{\rm t}( {t_{{\rm ph}}-t_{{\rm stc}}} ) $$
(B6)$$\beta _{{\rm rad}}{\rm} = 1 + \eta _{\rm s}( {G_{\rm s}-G_{{\rm stc}}} ) $$

The output electric power ΔP e can be obtained as follows:

(B7)$$\Delta P_{\rm e} = I_{\rm n}\alpha _{{\rm im}}G_{\rm s}A_{{\rm pv/t}}\eta _{{\rm ph}}$$

According to the literature, the outlet temperature of PV/T collectors can be obtained by the following equation:

(B8)$$t_{{\rm w, out}} = \left({t_{{\rm w, in}} + \displaystyle{\varepsilon \over k}} \right)\exp \left({\displaystyle{N \over {m_{\rm t}c_{{\rm pw}}}}\displaystyle{k \over \theta }L_{\rm w}} \right)-\displaystyle{\varepsilon \over k}$$

The heat absorbed by PV/T collectors can be obtained by the following equations:

(B9)$$Q_{{\rm pt}} = m_{\rm t}c_{{\rm pw}}( {t_{{\rm w, out}}-t_{{\rm w, in}}} ) $$
(B10)$$\eta _{{\rm th}} = \displaystyle{{Q_{{\rm pt}}} \over J}$$

Appendix C

In this paper, the PHST model of desiccant wheel is built based on some assumptions (Ma et al., Reference Ma, Xie, Li, Zhang, Liu and Luo2023a, Reference Ma, Xie, Wang, Min, Luo and Cai2023b, Reference Ma, Xie, Wang, Liu and Ding2023c, Reference Ma, Xie, Song, Liu, Luo and Wang2023d, Reference Ma, Xie, Min, Chen, Liu, Wang, Ding and Cai2023e, Reference Ma, Xie, Min, Liu, Wang, Ding and Luo2023f). The enthalpy of PCM can be obtained by the following equation:

(C1)$$h = c_{{\rm pcm}}( {t_{{\rm pcm}}-273.15} ) + \Delta H_{{\rm pcm}}$$

According to the energy conservation, the heat transfer equation of PCM can be obtained by the following equation:

(C2)$$\displaystyle{{k_{\rm s}} \over r}\displaystyle{\partial \over {\partial r}}\left({r\displaystyle{{\partial t} \over {\partial r}}} \right) = \rho _{\rm s}c_{{\rm pcm}}\displaystyle{{\partial T( {r, \;t} ) } \over {\partial t}}$$

The heat transfer equation of PHST can be obtained by the following equation:

(C3)$$\displaystyle{{\alpha h} \over {\alpha t}} + v_{\rm y}\displaystyle{{\alpha h} \over {\alpha y}} = \displaystyle{\partial \over {\partial y}}\left({\lambda \displaystyle{{\partial t} \over {\partial y}}} \right) + \displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\left({r\lambda \displaystyle{{\partial t} \over {\partial r}}} \right)$$

The thermal balance equation of PHST can be obtained by the following equation:

(C4)$$\displaystyle{{{\rm d}t_{{\rm tank}}} \over {{\rm d}t}} = \displaystyle{{Q_{{\rm in, tank}}-Q_{{\rm out, tank}}} \over {c_{{\rm mean}}}}$$

The above equation can be further expressed as

(C5)$$\displaystyle{{{\rm d}t_{{\rm tank}}} \over {{\rm d}t}} = \displaystyle{{Q_{{\rm flow}}{\rm} + Q_{{\rm hx}}-Q_{{\rm loss, \ top}}-Q_{{\rm loss, \ bottom}}-Q_{{\rm loss, \ edges}}} \over {c_{{\rm mean}}}}$$

The heat transfer rate of fluid flowing into PHST can be obtained as follows:

(C6)$$Q_{{\rm flow}}{\rm} = m_{{\rm tank, in}}c_{{\rm p, fluid}}( {t_{{\rm in, tank}}-t_{{\rm tank}}} ) $$

The heat transfer rate of fluid flowing into the immersed heat exchanger can be obtained by the following equation:

(C7)$$Q_{{\rm hx}}{\rm} = \eta _{{\rm hx}}m_{{\rm hx, in}}c_{{\rm p}, {\rm hx}}( {t_{{\rm in, hx}}-t_{{\rm tank}}} ) $$

The outlet temperature from the heat exchanger can be obtained as follows:

(C8)$$Q_{{\rm hx}}{\rm} = m_{{\rm hx, in}}c_{{\rm p}, {\rm hx}}( {t_{{\rm out, hx}}-t_{{\rm in, hx}}} ) $$

The heat transfer rate between PHST and the ambient temperature at the top, edges and bottom of PHST can be obtained by the following equations:

(C9)$$\left\{{\matrix{ {Q_{{\rm loss}, {\rm top}} = A_{{\rm top}}U_{{\rm top}}( {t_{{\rm tank}}-t_{{\rm env, \ top}}} ) } \hfill \cr {Q_{{\rm loss}, {\rm bottom}} = A_{{\rm bottom}}U_{{\rm bottom}}( {t_{{\rm tank}}-t_{{\rm env, \ bottom}}} ) } \hfill \cr {Q_{{\rm loss}, {\rm edges}} = A_{{\rm edges}}U_{{\rm edges}}( {t_{{\rm tank}}-t_{{\rm env, \ edges}}} ) } \hfill \cr } } \right.$$

References

Alberti, L, Antelmi, M, Angelotti, A and Formentin, G (2018) Geothermal heat pumps for sustainable farm climatization and field irrigation. Agricultural Water Management 195, 187–200.CrossRefGoogle Scholar
Baniasadi, E, Ziaei-Rad, M, Behvand, MA and Javani, N (2023) Exergy-economic analysis of a solar-geothermal combined cooling, heating, power and water generation system for a zero-energy building. International Journal of Hydrogen Energy 128, 175–210.Google Scholar
Blázquez, CS, Borge-Diez, D, Nieto, IM, Maté-González, MÁ, Martín, AF and González-Aguilera, D (2022) Geothermal heat pumps for slurry cooling and farm heating: impact and carbon footprint reduction in pig farms. Sustainability 14, 5792.CrossRefGoogle Scholar
Costantino, A, Fabrizio, E, Biglia, A, Cornale, P and Battaglini, L (2016) Energy use for climate control of animal houses: the state of the art in Europe. Energy Procedia 101, 184–191.CrossRefGoogle Scholar
Costantino, A, Fabrizio, E, Villagrá, A, Estellés, F and Calvet, S (2020) The reduction of gas concentrations in broiler houses through ventilation: assessment of the thermal and electrical energy consumption. Biosystems Engineering 199, 135–148.CrossRefGoogle Scholar
Deeken, HF, Lengling, A, Krommweh, MS and Büscher, W (2023) Improvement of piglet rearing's energy efficiency and sustainability using air-to-air heat exchangers-a two-year case study. Energies 16, 1799–1821.CrossRefGoogle Scholar
Haeussermann, A, Hartung, E, Jungbluth, T, Vranken, E, Aerts, J and Berckmans, D (2007) Cooling effects and evaporation characteristics of fogging systems in an experimental piggery. Biosystems Engineering 97, 395–405.CrossRefGoogle Scholar
Hu, Z, Yang, Q, Tao, Y, Shi, L, Tu, J and Wang, Y (2023) A review of ventilation and cooling systems for large-scale pig farms. Sustainable Cities and Society 89, 104372.CrossRefGoogle Scholar
Ibanez, M, Cabeza, LF, Solé, C, Roca, J and Nogués, M (2006) Modelization of a water tank including a PCM module. Applied Thermal Engineering 26, 1328–1333.CrossRefGoogle Scholar
Jia, CX, Dai, YJ, Wu, JY and Wang, RZ (2006) Experimental comparison of two honeycombed desiccant wheels fabricated with silica gel and composite desiccant material. Energy Conversion and Management 47, 2523–2534.CrossRefGoogle Scholar
Johnson, J, Martin, K, Pohler, K and Stewart, K (2016 a) Effects of rapid temperature fluctuations prior to breeding on reproductive efficiency in replacement gilts. Journal of Thermal Biology 61, 29–37.CrossRefGoogle ScholarPubMed
Johnson, JS, Sapkota, A and Lay J, (2016 b) Rapid cooling after acute hyperthermia alters intestinal morphology and increases the systemic inflammatory response in pigs. Journal of Applied Physiology 120, 1249–1259.CrossRefGoogle ScholarPubMed
Krommweh, MS, Rösmann, P and Büscher, W (2014) Investigation of heating and cooling potential of a modular housing system for fattening pigs with integrated geothermal heat exchanger. Biosystems Engineering 121, 118–129.CrossRefGoogle Scholar
Kupchuk, I and Telekalo, N (2022) Technical and Technological Prerequisites for the Introduction of Autonomous Energy Systems of Agro-Industrial Enterprises Using Renewable Energy Sources. Latvia: Baltija Publishing.CrossRefGoogle Scholar
Kwak, Y, Shin, H, Kang, M, Mun, SH, Jo, SK, Kim, SH and Huh, JH (2021) Energy modelling of pig houses: a South Korean feasibility study. Energy Strategy Reviews 36, 100672.CrossRefGoogle Scholar
Lapertot, A, Cuny, M, Kadoch, B and Le Métayer, O (2021) Optimization of an earth-air heat exchanger combined with a heat recovery ventilation for residential building needs. Energy and Buildings 235, 110702.CrossRefGoogle Scholar
Licharz, H, Rösmann, P, Krommweh, MS, Mostafa, E and Büscher, W (2020) Energy efficiency of a heat pump system: case study in two pig houses. Energies 13, 662.CrossRefGoogle Scholar
Liu, L, Tai, M, Yao, W, Zhao, R and Shen, M (2021) Effects of heat stress on posture transitions and reproductive performance of primiparous sows during late gestation. Journal of Thermal Biology 96, 102828.CrossRefGoogle ScholarPubMed
Lontoc, CA, Punay, LCL, Cajano, PJ and Vega, RS (2018) Comparative performance of sows housed with and without evaporative cooling system at temperature humidity index of 73–83. Journal of Veterinary and Animal Sciences 42, 77–84.Google Scholar
Ma, H, Liang, N, Liu, Y, Luo, X, Hou, C and Wang, G (2021 a) Experimental study on novel waste heat recovery system for sulfide-containing flue gas. Energy 227, 120479.CrossRefGoogle Scholar
Ma, H, Liang, N, Zhang, N, Luo, X, Hou, C and Wang, G (2021 b) Simulation of a novel waste heat recovery system with sulfide-containing flue gas. Applied Thermal Engineering 187, 116556.CrossRefGoogle Scholar
Ma, H, Xie, Y, Duan, K, Song, X, Ding, R and Hou, C (2022) Dynamic control method of flue gas heat transfer system in the waste heat recovery process. Energy 259, 125010.CrossRefGoogle Scholar
Ma, H, Xie, Y, Li, A, Zhang, T, Liu, Y and Luo, X (2023 a) A review on the effect of light-thermal-humidity environment in sow houses on sow reproduction and welfare. Reproduction in Domestic Animals 58, 1–23.CrossRefGoogle ScholarPubMed
Ma, H, Xie, Y, Wang, S, Min, K, Luo, X and Cai, W (2023 b) Comparison of operation characteristics of a new spray cooling system based on PV/T and heat recovery in sow houses in five climate regions of China. Energy and Buildings 296, 113411.CrossRefGoogle Scholar
Ma, H, Xie, Y, Wang, S, Liu, Y and Ding, R (2023 c) Exergy analysis of a new spray cooling system-based PV/T and heat recovery with application in sow houses. Solar Energy 262, 111828.CrossRefGoogle Scholar
Ma, H, Xie, Y, Song, X, Liu, Y, Luo, X and Wang, S (2023 d) Investigation on dynamic mathematical model and control method of flue gas heat exchange system. Engineering Computations 40, 434–456.CrossRefGoogle Scholar
Ma, H, Xie, Y, Min, K, Chen, Y, Liu, Y, Wang, S, Ding, R and Cai, W (2023 e) Investigation on the control strategy of new spray cooling system based on PV/T and heat recovery in sow houses: as a case study in Nanchang, China. Renewable Energy 219, 119472.CrossRefGoogle Scholar
Ma, H, Xie, Y, Min, K, Liu, Y, Wang, S, Ding, R and Luo, X (2023 f) Performance and optimization of a new spray cooling system with PV/T and heat recovery in sow houses: a case study in Nanchang, China. Applied Thermal Engineering 232, 121030.CrossRefGoogle Scholar
Mahmoud, BA, Houcine, I, Guizani, AA and Maalej, M (2005) Efficiency investigation of a new-design air solar plate collector used in a humidification–dehumidification desalination process. Renewable Energy 30, 1309–1327.Google Scholar
Moon, BE, Kim, HT, Nah, KD, Kim, JH and Kim, HT (2015) Analysis of internal environment in an enclosed pig house applied with energy recovery ventilator. Journal of Agriculture and Life Science 49, 163–175.CrossRefGoogle Scholar
Moon, BE, Lee, MH, Kim, HT, Choi, TH, Kim, YB, Ryou, YS and Kim, HT (2017) Evaluation of thermal performance through development of an unglazed transpired collector control system in experimental pig barns. Solar Energy 157, 201–215.CrossRefGoogle Scholar
Mun, H-S, Ahmed, ST, Islam, MM, Park, K-J and Yang, C-J (2015) Retrofitting of a pig nursery with solar heating system to evaluate its ability to save energy and reduce environmental pollution. Engineering in Agriculture, Environment and Food 8, 235–240.CrossRefGoogle Scholar
Mun, HS, Dilawar, MA, Jeong, MG, Rathnayake, D, Won, JS, Park, KW, Lee, SR, Ryu, SB and Yang, CJ (2020) Effect of a heating system using a ground source geothermal heat pump on production performance, energy-saving and housing environment of pigs. Animals 10, 2075–2098.CrossRefGoogle ScholarPubMed
Mun, HS, Dilawar, MA, Rathnayake, D, Chung, IB, Kim, CD, Ryu, SB, Park, KW, Lee, SR and Yang, CJ (2021) Effect of a geothermal heat pump in cooling mode on the housing environment and swine productivity traits. Applied Sciences 11, 10778.CrossRefGoogle Scholar
Nakomcic-Smaragdakis, B, Stajic, T, Cepic, Z and Djuric, S (2012) Geothermal energy potentials in the province of Vojvodina from the aspect of the direct energy utilization. Renewable and Sustainable Energy Reviews 16, 5696–5706.CrossRefGoogle Scholar
Niu, K, Zhong, J and Hu, X (2024) Impacts of climate change-induced heat stress on pig productivity in China. Science of the Total Environment 908, 168215.CrossRefGoogle ScholarPubMed
Opderbeck, S, Keßler, B, Gordillio, W, Schrade, H, Piepho, HP and Gallmann, E (2020) Influence of a cooled, solid lying area on the pen fouling and lying behavior of fattening pigs. Agriculture 10, 307.CrossRefGoogle Scholar
Parois, SP, Cabezón, FA, Schinckel, AP, Johnson, JS, Stwalley, RM and Marchant-Forde, JN (2018) Effect of floor cooling on behavior and heart rate of late lactation sows under acute heat stress. Frontiers in Veterinary Science 5, 223.CrossRefGoogle ScholarPubMed
Redelinghuys, LG, Tshamala, MC and Hans, TM (2023) Performance of an adiabatic pre-cooling system for concentrating solar power plants in arid areas. Applied Thermal Engineering 231, 120819.CrossRefGoogle Scholar
Riskowski, G, Shaffer, CS and Harrison, PC (2017) Effect of conductive cooling pads on heat and moisture production of gilts in hot and thermoneutral environments. Agricultural Engineering International: CIGR Journal 19, 13–19.Google Scholar
Romanini, CEB, Tolon, YB, Nääs, IDA and Moura, DJ (2008) Physiological and productive responses of environmental control on housed sows. Scientia Agricola 65, 335–339.CrossRefGoogle Scholar
Santonja, GG, Georgitzikis, K, Scalet, BM, Montobbio, P, Roudier, S and Sancho, LD (2017) Best available techniques (BAT) reference document for the intensive rearing of poultry or pigs. EUR 28674 EN 11, 898.Google Scholar
St-Pierre, NR, Cobanov, B and Schnitkey, G (2003) Economic losses from heat stress by US livestock industries. Journal of Dairy Science 86, E52–E77.CrossRefGoogle Scholar
Sultan, M, Miyazaki, T, Mahmood, MH and Khan, ZM (2018) Solar assisted evaporative cooling based passive air-conditioning system for agricultural and livestock applications. Journal of Engineering Science and Technology 13, 693–703.Google Scholar
Tabase, RK (2019) Mimicking indoor climate dynamics and ammonia emissions in a pig housing compartment using artificial pigs and an automatic urea spraying installation. Agricultural Engineering International: CIGR Journal 21, 40–50.Google Scholar
Tabase, RK, Millet, S, Brusselman, E, Ampe, B, Sonck, B and Demeyer, P (2018) Effect of ventilation settings on ammonia emission in an experimental pig house equipped with artificial pigs. Biosystems Engineering 176, 125–139.CrossRefGoogle Scholar
Tabase, RK, Bagci, O, De Paepe, M, Aarnink, AJ and Demeyer, P (2020) CFD simulation of airflows and ammonia emissions in a pig compartment with underfloor air distribution system: model validation at different ventilation rates. Computers and Electronics in Agriculture 171, 105297.CrossRefGoogle Scholar
Tajudeen, H, Moturi, J, Hosseindoust, A, Ha, S, Mun, J, Choi, Y, Sa, S and Kim, J (2022) Effects of various cooling methods and drinking water temperatures on reproductive performance and behavior in heat stressed sows. Journal of Animal Science and Technology 64, 782–793.CrossRefGoogle ScholarPubMed
TESS Library Documentation (2006) Thermal Energy System Specialists. TESS Library Documentation.Google Scholar
Wang, Y, Yang, H, Chen, H, Yu, B, Zhang, H, Zou, R and Ren, S (2023) A review: the development of crucial solar systems and corresponding cooling technologies. Renewable and Sustainable Energy Reviews 185, 113590.CrossRefGoogle Scholar
Wiegert, J, Knauer, M and Shah, SB (2022) Evaporative pad cooling impacts on barn environment and finishing pig performance. Applied Engineering in Agriculture 38, 351–359.CrossRefGoogle Scholar
Xie, Y, Min, K, Ma, H, Ding, R, Wang, S and Liu, Y (2024) Performance and economic comparison of three annual air-conditioning systems in sow houses. Applied Thermal Engineering 239, 122114.CrossRefGoogle Scholar
Yu, L, Shah, SB, Knauer, MT, Boyette, MD and Stikeleather, LF (2021) Comprehensive evaluation of a landscape fabric based solar air heater in a pig nursery. Energies 14, 7258–7295.CrossRefGoogle Scholar
Zhang, Q, He, S, Song, T, Wang, M, Liu, Z, Zhao, J, Gao, Q, Huang, X, Han, K and Qi, J (2023) Modelling of a PV system by a back-mounted spray cooling section for performance improvement. Applied Energy 332, 120532.CrossRefGoogle Scholar
Figure 0

Figure 1. New evaporative misting system constructed in this paper.

Figure 1

Table 1. Number meaning in the new evaporative misting system

Figure 2

Table 2. Main design and operating variables of the applied sow farm and the proposed system

Figure 3

Figure 2. Proposed system simulation model based on TRNSYS software.

Figure 4

Table 3. Some equipment and its variables in the proposed system simulation model

Figure 5

Table 4. Conditions adopted for verification based on the cited literature

Figure 6

Figure 3. Errors between the experimental dehumidification capacity and simulated data in the range of 18–40°C at the inlet of desiccant wheel.

Figure 7

Figure 4. Errors between the experimental and simulated outlet temperatures in the range of 28–40°C at the inlet of PV/T collectors.

Figure 8

Figure 5. Errors between experimental and simulated middle temperatures within 30 min after the heat exchange between PCM and circulating water.

Figure 9

Figure 6. Annual outdoor temperature changes in Guangzhou and indoor temperature changes under the regulation of the proposed system.

Figure 10

Figure 7. Solar radiation in Guangzhou and the solar fraction of the proposed system in the whole year.

Figure 11

Figure 8. Energy consumption of heating and cooling devices in the proposed system for a whole year.

Figure 12

Figure 9. Indoor time percentage at 18–27°C in the cooling season under different misting powers when MFWF is 7245 kg/h for the proposed system in Guangzhou.

Figure 13

Figure 10. Indoor time percentage at 18–27°C in the heating season under different MFWFs when the misting power is 40 kW for the proposed system in Guangzhou.

Figure 14

Figure 11. Energy consumption and exergy loss of the proposed system in Guangzhou under different load ratios in the cooling season.

Figure 15

Figure 12. Energy consumption and exergy loss of the proposed system in Guangzhou under different load ratios in the heating season.

Figure 16

Figure 13. HEC and EER of the proposed system in Guangzhou under different load ratios in the cooling season.

Figure 17

Figure 14. HEC and EER of the proposed system in Guangzhou under different load ratios in the heating season.

Figure 18

Figure 15. Annual SEB of the proposed system in Guangzhou under different load ratios.