Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T15:34:13.903Z Has data issue: false hasContentIssue false
  • English
  • Français

On the mathematical description of lactation curves

Published online by Cambridge University Press:  27 March 2009

A. J. Rook ,
J. France  and
M. S. Dhanoa
A. J. Rook
Affiliation:
AFRC Institute of Grassland and Environmental Research, North Wyke Research Station, Okehampton, Devon EX20 2SB, UK.
J. France
Affiliation:
AFRC Institute of Grassland and Environmental Research, North Wyke Research Station, Okehampton, Devon EX20 2SB, UK.
M. S. Dhanoa
Affiliation:
Plas Gogerddan, Aberystwyth, Dyfed SY23 3EB, UK
Get access Rights & Permissions [Opens in a new window]

Summary

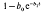The lactation curve may be represented mathematically by the general equation Y = Aϕ1(t)ϕ2(t), where A is a positive scalar, ϕ1,(t) is a positive monotonically increasing function with an asymptote at ϕ1 = 1, and ϕ2 is a monotonically decreasing function with an initial value of unity and an asymptote at ϕ2 = 0. Functions considered as candidates for ϕ1 were: (Mitscherlich), 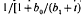(Michaelis-Menten), 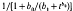(generalized saturation kinetic), 1/(1 + b0 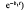(logistic), b0 exp 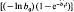(Gompertz) and [1+ tanh(b0 + b1t)]/2 (hyperbolic tangent). Candidates for ϕ2 were e–ct (exponential) and 1/(1 + ct) (inverse straight line). The 12 models thus obtained and Y = Atb e–ct (Wood's model) were fitted to whole-lactation data from 23 animals. Mitscherlich x exponential, Michaelis-Menten x exponential, logistic x exponential, logistic × inverse straight line and Wood's model all fitted well. For these models, expressions for time to peak, maximum yield, total yield over a finite lactation and relative decline at the midway point of the declining phase were obtained. The Mitscherlich x exponential model generally fitted better than Wood's model and, unlike Wood's model, gives simple algebraic formulae for all these summary statistics.

Type
Animals
Information
The Journal of Agricultural Science , Volume 121 , Issue 1 , August 1993 , pp. 97 - 102
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beale, E. M. L. (1960). Confidence regions in non linear estimation. Journal of the Royal Statistical Society 22, 41–88.Google Scholar
Dhanoa, M. S. (1981). A note on an alternative form of the lactation model of Wood. Animal Production 32, 349–351.Google Scholar
Elston, D. A., Glasbey, C. A. & Neilson, D. R. (1989). Non-parametric lactation curves. Animal Production 48, 331–339.Google Scholar
Emmans, G. C., Neilson, D. R. & Gibson, A. (1983). A general description of dairy cow potential. Animal Production 36, 546 (Abstract).Google Scholar
Grossman, M. & Koops, W. J. (1988). Multiphasic analysis of lactation curves in dairy cattle. Journal of Dairy Science 71, 1598–1608.CrossRefGoogle Scholar
Morant, S. V. & Gnanasakthy, A. (1989). A new approach to the mathematical formulation of lactation curves. Animal Production 49, 151–162.Google Scholar
Neal, H. D. St. C. & Thornley, J. H. M. (1983). The lactation curve in cattle: a mathematical model of the mammary gland. Journal of Agricultural Science, Cambridge 101, 389–400.CrossRefGoogle Scholar
Oldham, J. D. & Emmans, G. C. (1989). Prediction of responses to required nutrients in dairy cows. Journal of Dairy Science 72, 3212–3229.CrossRefGoogle ScholarPubMed
Papajcsik, I. A. & Bodero, J. (1988). Modelling lactation curves of Friesian cows in a subtropical climate. Animal Production 47, 201–207.Google Scholar
Ross, G. J. S. (1987). MLP Maximum Likelihood Program. Oxford: Numerical Algorithms Group.Google Scholar
Wood, P. D. P. (1967). Algebraic model of the lactation curve in cattle. Nature, London 216, 164–165.CrossRefGoogle Scholar
Wood, P. D. P. (1977). The biometry of lactation. Journal of Agricultural Science, Cambridge 88, 333–339.CrossRefGoogle Scholar