Sharaf al-Dīn ‘Alī Yazdī: Historian and Mathematician

Mahdi Farhani Monfared

doi:10.1080/00210860802246226

Sharaf al-Dīn ‘Alī Yazdī: Historian and Mathematician

Published online by Cambridge University Press: 01 January 2022

Mahdi Farhani Monfared

Show author details

Mahdi Farhani Monfared*: Affiliation:
Al-Zahra University, Tehran, Iran
*: [email protected]

Article contents

Abstract
Footnotes
References

Get access

Rights & Permissions

Abstract

The present article aims to shed light on the professional activities of the historian and mathematician Sharaf al-Dīn ‘Alī Yazdī and his 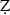afar-nāmah. In so doing, two questions are addressed: (1) Did Yazdī’s expertise in mathematics influence his historical narrative? (2) Did Yazdī simply expand on Ni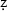ām al-Dīn Shāmī's 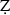afar-nāmah, composed some twenty years earlier? Comparing the frequency of quantitative and qualitative data in Yazdī's and Shāmī's 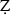afar-nāmahs, the article finds that although Yazdī made an effort to incorporate quantitative data in his history, his narrative is not particularly informed by his expertise in arithmetic. This seems, at first glance, a byproduct of a predominant tradition in the Islamic-Iranian historiography, which makes extensive use of literary techniques. The comparison between the two afar-nāmahs, however, suggests that both Yazdī and Shāmī subscribed to a notion of “accuracy” which bore little resemblance to its modern counterpart manifested in quantitative precision. Finally, the article concludes that the allegation of plagiarism against Yazdī is unfounded.

Type: Research Article
Information: Iranian Studies , Volume 41 , Issue 4: Sciences, Crafts, and the Production of Knowledge: Iran and Eastern Islamic Lands (ca. 184–1153 AH/800–1740 CE) , September 2008 , pp. 537 - 547

DOI: https://doi.org/10.1080/00210860802246226 [Opens in a new window]
Copyright: Copyright © Association For Iranian Studies, Inc 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Najm al-Din Yousefi translated this article from Persian.

References

¹ Yazdī, Sharaf al-Dīn ‘Alī, afar-nāmah, ed. by Abbasi, Mohammad, 2 vols. (Tehran, 1336/1957)Google Scholar

² Shāmī, Niẓām al-Dīn, afar-nāmah, ed. by Semnani, Panahi (Tehran, 1363/1984)Google Scholar. On the similarities between the two texts see Noubar, Ahmad Showqi, “Sanjesh va Tabīq Beyn-e dow afar-nāmah,” Journal of the Faculty of Letters and Humanities of the University of Tabriz, 28 (1355/1977): 435–436Google Scholar. Noubar emphasizes the close connection between the two books and provides a comparative chart (446–457); also see Nakhjavani, Hussein, “Ẓafarnāmaha,” Journal of the Faculty of Letters and Humanities of the University of Tabriz, 7 (1334/1956): 367Google Scholar.

³ Though the quantitative analysis and its application in historical research have been the object of theoretical inquiry, historians by and large seem to prefer qualitative/descriptive analysis. For the use of quantitative analysis in history, see Allswang, M. and Floud, R., An Introduction to Quantitative Methods for Historians (Princeton, 1973)Google Scholar. A recent contribution to this area is Hudson, Pat, History by Numbers: An Introduction to Quantitative Approaches (London and New York, 2000)Google Scholar. For a creative use of quantitative analysis in the history of early Islam, see Bulliet, Richard W., Conversion to Islam in the Medieval Period: An Essay in Quantitative History (Cambridge, MA, 1979)CrossRef Google Scholar.

⁴ Rāzī, Amīn Aḥmad, Haft Iqlīm, ed. by Fazel, Javad (Tehran, 1340/1962), 1: 150Google Scholar.

⁵ Samarqandī, Dawlatshāh, Tadhkara al-Shu‘arā, ed. by Browne, E. G. (Leiden, 1900/1318), 379Google Scholar.

⁶ Samarqandī, ‘Abd al-Razzāq, Mala‘ Sa‘dayn wa Majma‘ Barayn, ed. by Nava'i, Abd al-Husayn (Tehran, 1383/2004), 2: 589 (Part I)Google Scholar.

⁷ Navā'ī relates that he was six years old at the time of this meeting (850/1336–37). Barthold holds, however, that Navā'ī must have had about nine years of age (see Barthold, V. V., Four Studies on History of Central Asia, trans. by Minorski, V. (Leiden, 1993), 17Google Scholar. Elsewhere I have called into question Barthold's view, but further investigation confirms the validity of his judgment, see Monfared, Mahdi Farhani, Peyvand-e Sīyāsat va Farhang dar ‘Ar-e Zavāl-e Teymūrīyān va uhūr-e afavīyya (Tehran, 1381/2002), 169Google Scholar.

⁸ Navā'ī, Amīr Alīshīr, Majālis al-Nafā'is, ed. by Hekmat, Ali Asghar (Tehran, 1323/1944), 25Google Scholar.

⁹ Navā'ī, Majālis al-Nafā'is, 200.

¹⁰ A manuscript of this treatise is available in the Central Library of Tehran University (No.1035).

¹¹ The manuscripts of these treatises are available in the Āstān Quds Raavī’s library, Mashhad (No. 5608), and the Central Library of Tehran University (No. 3267), respectively.

¹² Kitāb al-Shāmil, 6–7. Magic squares have attracted the attention of mathematicians for over two millennia. The first extant magic square dates back to more than 2,300 years ago in China. A simple magic square can be defined as a sequence of numbers (1, 2, 3,…, n²) in an nXn matrix, such that every number is input no more than once, and the sum of numbers in each row, column, or diagonal is equal to the sum of numbers in every other row, column, or diagonal; for magic squares, see Sesiano, Jacques, “Herstellungsverfahren magischer Quadrate aus islamischer Zeit, I,” Sudhoffs Archiv für Geschichte der Medizin, 44 (1980): 187–196Google Scholar; and “Herstellungsverfahren magischer Quadrate aus islamischer Zeit, II,” Sudhoffs Archiv für Geschichte der Medizin, 65 (1981): 251–256Google Scholar; also Sesiano, , “Construction of Magic Squares Using the Knight's Move in Islamic Mathematics,” Archive for History of Exact Sciences, 58 (2003): 1–20CrossRef Google Scholar.

¹³ A manuscript of this work is available at the Library of Iranian Parliament (No. 855/1, 1a–26b).

¹⁴ Samarqandī, Tadhkara al-Shu‘arā, 379.

¹⁵ Terms such as gaz, gaz-e shar‘, gerah (or gurūh), and farsakh (or farsang) were used to measure distance while man and man-e Shar‘ were used for weight measurement. These terms are presented with their transliterated Persian names since no English equivalents are available for them.

¹⁶ Yazdī, afar-nāmah, 1: 16, 17.