Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T13:04:29.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Euclid's Elements, Courtly Patronage and Princely Education

Published online by Cambridge University Press:  01 January 2022

Sonja Brentjes
Sonja Brentjes*
Affiliation:
Department of Philosophy and Logic, University of Seville, Spain
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Persian tradition of Euclid's Elements is closely connected with the Arabic transmission of the work in Iran, Central Asia and India. This tradition has multiple starting points. Na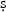īr al-Dīn 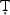ūsī's Arabic edition had a profound impact, but it was one of several Arabic versions that served as the basis for Persian translations. At the institutional level both the Arabic and the Persian traditions flourished in different spaces—at the courts, in the madrasa, and in the sphere of collectors. Emphasizing the continued importance of court patronage, this paper explores the specifics of spatial and temporal coordinates in the transmission and transformation of Euclid's Elements in Islamic Iran.

Type
Articles
Information
Iranian Studies , Volume 41 , Issue 4: Sciences, Crafts, and the Production of Knowledge: Iran and Eastern Islamic Lands (ca. 184–1153 AH/800–1740 CE) , September 2008 , pp. 441 - 463
Copyright
Copyright © Association For Iranian Studies, Inc 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Two magnitudes are called incommensurable if there is no integer that divides each of the two without a remainder. Magnitudes are called inexpressible when their ratio cannot be expressed as a ratio of two integers.

2 These new dates for Qāīzādah Rūmī' life were established by Ihsan Fazlıoglu, Istanbul. I thank Sally Ragep, Montreal for sharing this information with me. Fazlıoglu, Ihsan. “Osmanlı felsefe-biliminin arkaplanı: Semerkand matematik-astronomi okulu,” Dîvân lmî Araştırmalar, 14 (2003/1): 1–66Google Scholar. A revised English version will appear as “The Samarqand Mathematical-Astronomical School: A Basis for Ottoman Philosophy and Science,” Journal for the History of Arabic Science, 14 (2008): 3–68Google Scholar.

3 MS Hyderabad, Andhra Pradesh Government Oriental Manuscripts Library and Research Institute, Riyāī 496.

4 MS London, British Library, Or. 1514: f 3b, 10–15.

5 MS London, British Library, Or. 13838: f 2a, 12–2b, 5.

6 The Fihrist of Ibn al-Nadīm: A Tenth-Century Survey of Muslim Culture, trans. by Dodge, Bayard (New York, 1970), 2: 634Google Scholar.

7 Codex Leidensis 399, 1, Euclidis Elementa ex Interpretatione Al-Hadschdschadschii cum Commentariis Al-Narizii. Arabice et Latine Ediderunt Notisque Instruxerunt R. O. Besthorn et J. L. Heiberg, Partis I Fasciculus II (Haunia, 1892): 4.

8 De Young, Gregg, “The Arabic Version of Euclid's Elements by al-ajjāj ibn Yūsuf,” Zeitschrift für Geschichte der Arabisch-Islamischen Wissenschaften, 15 (2002/03): 125–164Google Scholar, 130.

9 The Fihrist, 2: 639, 710, 826–827.

10 The Fihrist, 2: 587.

11 Khaldūn, Ibn, The Muqaddimah: An Introduction to History, trans. by Rosenthal, Franz (New York, 1980), 2nd printing of 2nd ed., 3 vols., 3: 130Google Scholar.

12 The Fihrist, 2: 584.

13 The Fihrist, 2: 584.

14 Works of ancient Greek authors and treatises written by scholars from Islamic societies to be studied after Euclid's Elements and before Ptolemy's Almagest.

15 The Fihrist, 2: 635.

16 J. L. Berggren, “Patronage of the Mathematical Sciences in the Buyid Courts,” unpublished manuscript. I thank Len for allowing me to use his text.

17 Matvievskaya, G. P., Učenie o čisle na srednevekovom vostoke (Tashkent, 1967), 211–212Google Scholar.

18 Matvievskaya, Učenie o čisle na srednevekovom vostoke, 212–213.

19 Matvievskaya, G. P. and Rozenfel'd, B. A., Matematiki i astronomy musul'manskogo srednevekov'ja i ich trudy (VIII-XVII vv) (Moskva, 1985), 3 vols., 2: 161Google Scholar; Gregg De Young, Truncated Texts: Examples from the Euclidean Transmission, Forthcoming.

20 Crozet, P., “Al-Sijzī et les Éléments d'Euclide: Commentaires et d'autres démonstrations des propositions,” in Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque, ed. by Hasnawi, A., Elamrani-Jamal, A. and Aouad, M. (Leuven, Paris, 1997), 61–77Google Scholar.

21 Matvievskaya and Rozenfel'd, Matematiki, 2: 189.

22 De Young, Gregg, “Abū Sahl's Additions to Book II of Euclid's Elements,” Zeitschrift für Geschichte der Arabisch-Islamischen Wissenschaften, 7 (1991/92): 73–135, 78Google Scholar.

23 Berggren, J. L. and van Brummelen, G., “From Euclid to Apollonius: Al-Kūhī's lemmas to the Conics,” Zeitschrift für Geschichte der Arabisch-Islamischen Wissenschaften, 15 (2002/03): 165–174, 167–168Google Scholar.

24 Berggren, J. L. and van Brummelen, G.R., “Al-Kūhī's revision of Book I of Euclid's Elements,” Historia Mathematica, 32 (2005): 426–452CrossRefGoogle Scholar, 427–429.

25 al-Bayhaqī, Ẓahīr al-Dīn, Tārīkh al-ukamā', ed. by Muhammad, Mamduh Hasan (al-Qāhira, 1996/1417), 117Google Scholar.

26 ahīr al-Dīn al-Bayhaqī, Tārīkh al-ukamā’, 117.

27 Papazyan, A. D., “Ob odnoy rukopisi ‘Knigi spaseniya’ Abu-Ali Ibn-Sina,” Dokladov Akademii Nauk Armyanskoy SSR, xxiii (1956): 229–234, 231Google Scholar.

28 MS London, British Library, Or. 6572: f 53b, center text, lines 3–9; MS London, British Library, Add. 16830: f 207b3–10; Akhadova, M. A., “Geometričeskaya čast' knigi ‘Znaniya’ Ibn Sina,” Učenye Zapiski, Seriya Fiziko-Matematičeskikh Nauk 1 (1964): 143–204Google Scholar, 144.

29 Bayhaqī, Tārīkh, 70–71.

30 Avicenne, Le livre de science, trans. by Achena, Mohammad and Massé, Henri (Paris, 1958), 2: 91–239Google Scholar.

31 Akhadova, “Geometričeskaya čast',” 144–151.

32 Akhadova, “Geometričeskaya čast',” 152–160.

33 Akhadova, “Geometričeskaya čast',” 161–165.

34 Akhadova, “Geometričeskaya čast',” 166–172.

35 Akhadova, “Geometričeskaya čast',” 172–187.

36 Akhadova, “Geometričeskaya čast',” 187–190.

37 Akhadova, “Geometričeskaya čast',” 191–202.

38 Akhadova, “Geometričeskaya čast',” 202.

39 Papazyan, “Ob odnoy rukopisi,” 229–230.

40 Ellis, A. G. and Edwards, Edward, A Descriptive List of the Arabic Manuscripts Acquired by the Trustees of the British Museum Since 1894 (London, 1912), 11Google Scholar.

41 Ellis and Edwards, A Descriptive List.

42 MS London, British Library, Or. 6572: ff 53b–63b.

43 MS British Library, Or. 6572: f 64a.

44 MS British Library, Or. 6572: f 53b, 17–54b, 23.

45 Bayhaqī, Tārīkh, 155.

46 Smith, D. E., “Omar Khayyam and Saccheri,” Scripta Mathematica, 3 (1935): 5–10Google Scholar; Plooij, E. B., Euclid's Conception of Ratio and his Definition of Proportional Magnitudes as Criticized by Arabian Commentators (Rotterdam, 1950)Google Scholar; Amir-Moez, A. R., “Discussions of Difficulties in Euclid,” Scripta Mathematica, 24 (1959): 275–303Google Scholar; Jaouiche, K., “De la fécondité mathématique: d'Omar Khayyam à G. Saccheri,” Diogène, 57 (1967): 97–113Google Scholar; Jaouiche, K., La théorie des parallèles en pays d'Islam (Paris, 1986)Google Scholar; Rosenfeld, B. A., A History of Non-Euclidean Geometry (New York, 1988), 64–71CrossRefGoogle Scholar; Djebbar, A., L'émergence du concept de nombre réel positif dans l'épitre d'al-Khayyām (1048–1131) Sur l'explication des prémisses problématiques du livre d'Euclide (Paris: Université Paris-Sud, Prépublications Mathématiques d'Orsay, 97–38, 1997)Google Scholar; Vahabzadeh, B., “Omar Khayyam and the Concept of Irrational Number,” Farhang, 18 (2004/05): 125–134Google Scholar.

47 For a recent discussion of the concept of movement in ancient geometry and Khayyām's criticisms, see Vitrac, B., “Quelques remarques sur l'usage du mouvement en géométrie dans la tradition euclidienne: de Platon et Aristote à Omar Khayyām,” Farhang, 18 (2004/05): 1–56Google Scholar.

48 Akhadova, “Geometričeskaya čast',” 173–174; Akhadova, M., “Arifmetičeskaya čast' ‘Knigi Znaniya’ Ibn-siny [sic],” Učenye Zapiski, 12 (1964): 263–281Google Scholar, 272–276.

49 Matvievskaya and Rozenfel'd, Matematiki, 2: 316–317.

50 Bayhaqī, Tārīkh, 140–141.

51 Matvievskaya and Rozenfel'd, Matematiki, 2: 321; MS Paris, BnF, Ar. 2458: 9–11.

52 Matvievskaya and Rozenfel'd, Matematiki, 2: 321.

53 MS BnF, Ar. 2458: 9, 2.

54 Ragep, F. J., Naīr al-Dīn al-ūsī's Memoir on Astronomy (al-Tadhkira fi ‘ilm al-hay'a) (New York, Berlin, Heidelberg et al., 1993), 2 vols., 1: 23Google Scholar.

55 Ragep, Memoir, 1: 23.

56 Ragep, Memoir, 1: 23.

57 MS Oxford, Bodleian Library 448; Sezgin, Fuat, Geschichte des Arabischen Schrifttums (Leiden, 1974)Google Scholar 5: 114.

58 MS Dublin, Chester Beatty Library, 3424: f 1b, 3–5.

59 MS Oxford, Bodleian Library, 448: ff 1b, 5–2a, 4.

60 Matvievskaya and Rozenfel'd, Matematiki, 2: 394, 428.

61 MS London, British Library, Add. 233387, see for instance f 6a.

62 MS London, Staatsbibliothek, Or. fol. 256.

63 MS London, Staatsbibliothek, Or. fol. 256: f 5b, 9–11; MS London, British Library, Add. 7694: f 83b, 9–13.

64 MS London, Staatsbibliothek, Or. fol. 256: ff 32a, 4–42b, 10; MS London, British Library, Add. 7694: f 87b, 10.

65 MS London, British Library, Add. 7694: f 87b, 10–12.

66 Brentjes, S., “On the Persian Transmission of Euclid's Elements,” in La science dans le monde iranien à l'époque islamique, ed. by Vesel, Z., Beikbaghban, H. and de Crussol des Epesse, Thierry (Téhéran, 1998), 73–94, 78–80Google Scholar.

67 Matvievskaya and Rozenfel'd, Matematiki, 2: 476.

68 MS London, British Library, Or. 3143.

69 MS London, British Library, Or. 3143: f 25a, 7–8.

70 Shams al-Dīn al-Sakhawī, al-Daw' al-lamī‘ fi ahl a-qarn al-tasī‘ (Bayrut, s.d.), 5: 48; F. Jamil Ragep, “Qāīzāde al-Rūmī,” in Thomas Hockey (editor-in-chief), Virginia Trimble and Thomas R. Williams (Senior Editors), Biographical Encyclopedia of Astronomers, 2 vols. (New York, s.d.), 2: M–Z, 942.

71 MS London, British Library, Or. 3143: ff 25b, 12–26a, 21.

72 MS London, British Library, Or. 3143: f 26a, 7–12.

73 MS London, British Library, Or. 3143: ff 25b, 21–22; 26a, 12–20.

74 MS London, British Library, Or. 3143: ff 25b, 9–20; 26a, 3.

75 Timur and the Princely Vision: Persian Art and Culture in the Fifteenth Century, ed. by Lentz, Thomas W. and Lowry, Glenn D. (Los Angeles and Washington DC, 1989), 57–58Google Scholar, 79–103, 108–139.

76 Aubin, Jean, “Le Mécénat Timouride à Chiraz,” Studia Islamica, 8 (1957): 71–88CrossRefGoogle Scholar, 82–83.

77 MS London, British Library, Add. 27162: ff 340b–342b; 343a–344a. A further treatise on ‘ilm al-hay'a composed by Ghīyāth al-Dīn for Iskandar Sulān is found in Qum, see Fihrist nuskhahā-yi khaī-yi Kitābkhānah-yi ‘umūmī-yi arat-i Āyatollāh al-‘umā Najafī Mar‘ashī, ed. by Sayyid Mahmud Mar‘ashi and Sayyid Ahmad Husayni (Qum, 1395 q/1357 sh), jild 2: 210, n° 1015, 12: ff 262b–278b.

78 MS London, British Library, Add. 27162: f 343a, 2–3.

79 MS London, British Library, Add. 27162: f 343a, 3–4.

80 Soucek, P., “The Manuscripts of Iskandar Sultan,” in Timurid Art and Culture: Iran and Central Asia in the Fifteenth Century, ed. by Golombek, Lisa and Subtelny, Maria (Leiden, New York and Köln, 1992), 116–131Google Scholar.

81 MS London, British Library, Or. 1514: f 4b, 2–9.

82 MS British Library, Or. 1514: ff 5b, 15–16a, 4.

83 MS British Library, Or. 1514: ff70b, 16–71a, 6.

84 MS British Library, Or. 1514: ff 95a–95b; 98a.

85 MS British Library, Or. 1514: f 12a.

86 Sezgin, Geschichte des Arabischen Schrifttums, 5: 113.

87 MS London, British Library, Add 2357: ff 31–133.

88 Matvievskaya and Rozenfel'd, Matematiki, 2: 590.

89 Matvievskaya and Rozenfel'd, Matematiki, 2: 590.

90 MS London, British Library, Add. 21952: f 149a, 9–15.

91 MS London, British Library, I.O. Isl. 923: ff 71b–95a.

92 MS Cambridge, Harvard University, Arthur M. Sackler Museum, 1984.463: ff 54b, lower margin – 56a, left margin.

93 MS Sackler 1984.463: f 56a, left margin.