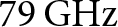Analysis of interference effects on CaCS-based radar systems

Abstract

This paper presents a comprehensive analysis of interference events in automotive scenarios based on radar systems equipped with communication-assisted chirp sequence (CaCS). First, it examines the impact of interference on radar and communication functionalities in CaCS systems according to the orientation of the investigated nodes. For this purpose, a graph-based approach is employed with MATLAB simulations to illustrate the potential occurrence of interference on the graph for communication functionality compared with their counterparts on radar. Second, the paper delves into the impact of interference on the synchronization between two communicating CaCS nodes. It extends a previous study to match the frequency of current radar sensors, where chirp estimation, an adjusted version of the Schmidl & Cox algorithm, and correlation are adopted to synchronize the transmitter and receiver of two CaCS communicating nodes in the time-frequency plane. The proposed synchronization method is finally verified by measurements at ${79}\,\mathrm{GHz}$ with a system-on-chip, where the resulting correlation metric and mean square error are illustrated as validation factors.

Introduction

This paper extends the study published at the 20th European Radar Conference (EuRAD) [1].

Radar sensors have seen widespread application across various domains due to their versatility in diverse operating conditions. The recent surge in developing safety mechanisms for road vehicles has sparked considerable interest in both industry and academia. This interest focuses on integrating and advancing driver-assistance systems (ADAS) to minimize accidents. The implementation of ADAS requires vehicles to be equipped with multiple radar sensors to ensure reliable autonomous object detection. However, achieving effective autonomous object detection necessitates equipping each car with multiple radar sensors. This requirement, in turn, increases the potential for interference from signals emitted by other sensors in the environment [2, 3]. Therefore, numerous studies have explored various methods to mitigate interference among radars operating in the same environment, considering factors like temporal, spectral, and spatial separation of the interferers [4, 5]. Time-domain techniques, like clipping, have proven effective in reducing interference impact on radar systems by limiting the amplitude of strong interfering signals [6]. However, clipping can influence the radar sensitivity in detecting weak targets. Another approach for interference mitigation in CS-based radar systems involves randomly altering the timing of the chirp sequence to decouple frequency ramps within the same time slot. In the frequency domain, frequency hopping has emerged as a prominent option for interference mitigation in automotive scenarios. This technique involves switching the frequency of radars between a predefined set of frequencies. It can be implemented using random frequency selection or hopping based on a predetermined pattern [7]. Furthermore, graph-based investigations have analyzed the impact of mutual interference on the sensors that share the same environment based on their orientations, frequency bands, transmit power, signal durations, and field of view (FoV), and colors on the graph have been developed to support it [8]. One potential technique to minimize interference is the integration of communication symbols within radar signals, enabling sensors to communicate in advance and avoid potential transmission overlaps [9, 10]. This communication involves exchanging crucial parameters such as bandwidth, signal duration, and carrier frequency. Given the widespread use of chirp modulation schemes in modern radar sensors, numerous studies have explored the integration of communication data and its effects on radar signal processing [11–13]. These studies propose communication as an auxiliary function to enhance radar functionalities, representing the system as a communication-assisted chirp sequence (CaCS)-based radar concept. Partial chirp modulation is a convenient approach in this context, where chirps are modulated in smaller sectors to limit the impact on radar operations while ensuring the transmitted data meets the service requirements [11]. Although the bandwidth allocated for communication is narrow, interference can still affect the demodulation process and synchronization in the initial stages. Consequently, the impact of interference is analyzed based on its overlap degree in the studied scenario. In this sense, the paper in [1] presented a case study of interference impacts on synchronization between communicating vehicles in the baseband. The study adopted a chirp-like approach [14, 15], where several CaCS nodes transmit their signals concurrently. In addition, the paper in [1] introduced an interference detection scheme to reallocate the communication receiver in the time-frequency plane. Apart from that, this paper extends the study in [1] and employs measurements at ${79}\,\mathrm{GHz}$, where the results align with their counterparts from the study in [1]. Besides, a graph-based scheme is presented to highlight the interference impact on communication compared with its counterpart on the radar with illustrations on the graph.

The remainder of the paper is organized as follows. Section “CaCS radar” briefly introduces the approach of CaCS-based radar systems. Section “Interference detection and synchronization” presents a graph-based approach to the interference influence on radar and communication. Besides, the interference detection scheme is proposed, and the impact on the synchronization between the communicating vehicles is analyzed. The results are presented in section “Measurement results,” and conclusions are drawn in section “Conclusion.”

CaCS radar

System design and frame structure

In Fig. 1, a sketch representing an example of the investigated scenario is illustrated. Four nodes are adopted for the ease of simplicity. Each node comprises an operational configuration to facilitate radar and communication features. N ₁ emerges as a pivotal actor with an active radar alongside a separate communication receiver, driven by the dual functionality of target detection and concurrent communication engagement with other nodes, such as N ₂. Meanwhile, N ₂, equipped with its dedicated communication receiver, operates to capture the signal from N ₁ and extracts the information sent from N ₁ to enable data exchange for their signal properties and traffic status of the surroundings. Simultaneously, N ₃ and N ₄, on the other hand, are characterized by the activation of their radar transceivers, eliciting a deliberate generation of interference aimed at N ₂.

Figure 1. Exemplary scenario in automotive applications. N ₁ represents the node that is responsible for radar and communication transmission. N ₂ is the node where the valuation of communication data takes place. N ₃ and N ₄ illustrate a possible interference events aimed at N ₂. The blue line represents communication transmission, while the black and green counterparts represent the detection in the surroundings. Red lines illustrate possible interference events.

The signal frame for the proposed CaCS-based radar systems consists of two sub-frames. Initially, a preamble-based chirp signal is transmitted to ensure synchronization between the transmitter of one node and the receiver of another. This synchronization section includes a predetermined number of up- and down-chirps [14] and is adjusted at the beginning for each sensor transmitting in the same environment. Following this, the signal used for CaCS-based radar systems is transmitted to achieve both communication and sensing functionalities. A sequence of multiple modulated chirps, denoted as $Q_\mathrm{rc}$ with index ${q_\mathrm{rc}~\in~\{0,1,\dots, Q_\mathrm{rc}-1\}}$, a time duration $T_\mathrm{C}$, and equal pauses between each, is transmitted to enable relative speed estimation at the radar receiver. An exemplary chirp sequence with a time repetition interval $T_\mathrm{RRI}$ and a duration of ${T^\mathrm{rc}_\mathrm{Seq}=Q_\mathrm{rc}T_\mathrm{RRI}}$ is depicted in Fig. 2. As illustrated, the communication symbols are modulated in a narrow sector at the upper part of each chirp, within a limited bandwidth $B_\mathrm{com}$ and time duration $T_\mathrm{com}$. These communication symbols are assigned to different phases according to quadrature phase shift keying. Moreover, at the beginning of the frame, a set of up- and down-chirps is allocated for synchronization within the duration $T^\mathrm{sync}_\mathrm{Seq}$. This structure ensures efficient synchronization and accurate relative speed estimation, thereby enhancing the overall performance of the CaCS-based radar systems.

Figure 2. Representation of CaCS-based radar system. Structure of the transmit CaCS-based signal, including the pattern for the synchronization and the dedicated chirps for both radar and communication functionalities [1].

Interference on graph

Radar sensors on different vehicles face challenges from various sources of interference in the environment. For this purpose, a graph-based approach is employed to clarify the degree of interference between the nodes using principles from graph theory [8, 15, 16]. The nodes are modeled as a graph to represent the aforementioned CaCS-based systems with either radar or communication functionality, and edges illustrate interference between nodes. A graph, denoted as $G = (V, E)$, consists of a set of vertices $V = \{v_1, \ldots, v_N\}$ and a set of edges $E \subseteq V \times V$, representing connections between vertices. The edge set E contains tuples $(v_i, v_j)$ for which nodes v_i and v_j are connected, where the number of edges is $|E| = M$. A graph can be categorized as directed if its edges have a defined direction or undirected with no specified orientation for the edges. Undirected graphs are investigated since the sensors can cause interference and simultaneously be a victim. The graph-based interference modeling for CaCS-based nodes is developed based on multiple critical factors, including signal duration, bandwidth, transmit power, and FoV. Signal duration refers to the temporal extent of sensor signals, dictating the duration of potential interference events. A realistic-based scenario is shown in Fig. 3, where sensors emit periodic signals with finite durations, within the investigated bandwidth and limited transmitted power. Interference occurs when signals overlap in time and frequency with enough strength, leading to potential disruptions in sensor readings during the signal processing. Additionally, the FoV range of sensors is incorporated into the modeling framework. The FoV defines the angular coverage of sensor measurements, representing the spatial extent to which sensors can detect objects. Interference is considered between sensors whose operational ranges intersect within the FoV angle range of each other.

Figure 3. Interference analysis of CaCS-based systems according to graph and color concepts. (a) Graph-based illustration of a scenario with 3 vehicles and 12 nodes from the perspective of the radar transceiver. (b) Graph-based illustration of a scenario with 3 vehicles and 12 nodes from the perspective of the communication receiver. (c) Graph-based illustration of a scenario with 10 vehicles and 40 nodes from the perspective of the radar transceiver with color mapping, leading to 3 unique colors. (d) Graph-based illustration of a scenario with 10 vehicles and 40 nodes from the perspective of the communication receiver with color mapping, leading to 2 unique colors. However, only the desired vehicle is illustrated since the scenario spanned widely in (c) and (d). (e) Comparison of interference occurrence between radar $\mathrm{int}_\mathrm{rad}$ and communication $\mathrm{int}_\mathrm{com}$ cases. (f) Probability of error occurrence based on interference grade for radar and communication.

Since the proposed CaCS nodes also comprise a communication part with limited bandwidth $B_\mathrm{com}\lt \lt B$,this allocation might restrict the amount of information that can be transmitted, but at the same time the interference event based on the same criteria of the limited bandwidth. In contrast, the radar part typically operates with access to a broader frequency spectrum, spanning about $B = {4}\,\mathrm{GHz}$ within 79–81 GHz. This wide bandwidth allows radar signals to occupy a larger portion of the frequency spectrum, enabling high-resolution sensing and detection capabilities. However, radar detections can be restricted by interference events. Therefore, employing techniques to mitigate the effects of interference is a vital feature for safe monitoring of the environment. For example, a scenario with 3 vehicles with four sensors in each leads to 12 nodes in the scenario. The distance threshold for interference is set at 150 m, defining the maximum allowable distance between nodes for interference to occur. Each sensor generates signals for communication and sensing purposes. These signals have specific durations, with each node generating 128 chirps. For example, signal durations range from 10 to 100 μs, with an interval of 2 μs between consecutive chirps. Each sensor operates within a defined center frequency range, randomly assigned between 76 and 81 GHz. The receiver in the network has a bandwidth limitation of 100 MHz, constraining the communication bandwidth. Furthermore, the sensors have a defined FoV, with an angle range of −80 to 80^∘, dictating the angular span over which each sensor can perceive its environment. As depicted in Fig. 3(a) and (b), the interference between CaCS nodes with radar functionality can occasionally be severe, where five interference cases are introduced. On the other hand, if the interference is investigated within the communication section, merely one interference event is observed for the same parameters above. An extension of the scenario with 10 vehicles, each equipped with 4 sensors leads to 40 nodes in the scenario. In Fig. 3(c), the connections between nodes are performed and illustrated based on interference that occurred from the perspective of node 8. Since the bandwidth and time duration of the investigated radar signal is considerable compared with the communication section, node 8 undergoes five interference cases, where $|E^{8}_\mathrm{rad}| = 5$. To minimize or mitigate this impact, a coloring approach on the graph is recommended to coordinate the resources between the nodes with a degree of orthogonality C relative to the number of unique colors applied to the graph [16]. According to this approach, two connected nodes cannot possess the same color, leading to three colors with $C_\mathrm{rad} = 3$. On the other hand, Fig. 3(d) depicts the same investigation from the perspective of the communication receiver. In this case, node 8 can merely undergo two interference cases with $|E^{8}_\mathrm{com}| = 2$, and two colors $C_\mathrm{com} = 2$ are needed to coordinate the scenario. It should be mentioned that the number of edges E and colors C are usually presented according to the complete graph. However, only one node has been considered for the sake of simplicity. Overall, the results indicate the importance of establishing communication between the CaCS-based nodes. Since the impact of interference on communication is so minimal, the nodes can communicate beforehand and adjust their parameters to avoid distorting their radar functionalities. Furthermore, the impact of interference on node 8 is analyzed further in Fig. 3(e) and (f). The occurrence of interference for radar and communication functionalities $\mathrm{int}_\mathrm{rad}$, $\mathrm{int}_\mathrm{com}$ caused by other nodes in the surroundings is illustrated in Fig. 3(e). In this term, the interference in communication at node 8 occurred about ${7}{\%}$ compared with its radar counterpart, which occurred about ${68}{\%}$ among $n_\mathrm{snap} = 100$ snapshots. Figure 3(f) depicts the probability of interference occurrence relative to the number of interferers in the scenario. For node 8, about ${85}{\%}$ of the snapshots undergone no interference for $\mathrm{int}_\mathrm{com}$ and less than ${35}{\%}$ for its radar counterpart, where eight interferers might contribute to those effects in some rare cases, less than ${5}{\%}$. It should be noted that the orientation of the investigated nodes has been arbitrarily chosen, and concrete information regarding the automotive scenario can lead to lower interference impacts on radar and communication functionalities. Besides, the decision to have interference in the scenario has been connected with the geometrical location of the nodes, the power level of the interferers, and the overlapping of their signal in the time-frequency plane within the receiver bandwidth of the investigated node.

Interference detection and synchronization

While the chirp time duration in CaCS-based radar systems can accommodate a limited number of coexisting signals [17], interference can significantly hinder synchronization and communication functions. Figure 4 illustrates an example of signal distribution within the time-frequency plane, where the worst-case scenario occurs when the up- and down-chirps dedicated to synchronization in each transmit signal overlap within the same time interval. In this scenario, three patterns are depicted with varying chirp rates $\{\mu_1$, µ ₂, $\mu_3, \mu_4\}$, chirp durations $\{T_\mathrm{C_1}$, $T_\mathrm{C_2}$, $T_\mathrm{C_3}, T_\mathrm{C_4}\}$, and bandwidths $\{B_{1}$, B ₂, $B_3, B_4\}$. The communication methods proposed in [12] utilize a limited-band communication receiver, similar to those in current automotive radar sensors. Consequently, only the sector between the dashed lines in Fig. 4, within the bandwidth $B_\mathrm{com}$, is further processed in the signal processing chain.

Figure 4. Visualization of several chirp signals with different parameters in the time-frequency plane: chirp rates $\{\mu_1$,  µ ₂,  µ ₃,  $\mu_4\}$, time durations $\{T_\mathrm{C_1}$, $T_\mathrm{C_2}$, $T_\mathrm{C_3},~T_\mathrm{C_4}\}$, and bandwidths $\{B_{1}$, B ₂, $B_3, B_4\}$ [1].

Correlation approach

According to the study presented in [1], a promising approach to synchronize the transmitter and receiver of communicating CaCS nodes in an interfering environment involves creating a codebook that incorporates the parameters of the signals. This codebook-based method enables the detection of interference at the beginning of the procedure, with synchronization applied in subsequent steps. The two-stage interference detection and synchronization method begins with chirp rate estimation of the signals, where the slopes are assigned within the predetermined codebook. Initially, the interference is identified by comparing incoming signals with the entries in the codebook, allowing for the quick detection of potential conflicts. Once interference is detected, the next step comprises applying correlation to the chosen detected patterns within the codebook. This correlation process synchronizes the receiver of one CaCS node with one of the desired transmit signals, facilitating reliable communication. This method offers several advantages, where the system can quickly identify and resolve interference events. Besides, the use of chirp rate estimation enhances the robustness in environments with high levels of signal interference.

Chirp rate estimation

In this framework, all the signals overlapping within one evaluated time duration $T_\mathrm{C}$ can be detected if each adopts a unique chirp rate. The detected chirp rates are estimated using the fast quadratic phase transform (FQPT) [18], in which an adaption from the conventional discrete Fourier transform (DFT) is adopted to estimate the slopes of the receive signals within the limited bandwidth on the communication receiver, as depicted in Fig. 5. After filtering the input signal according to $B_\mathrm{com}$ within the longest time duration of the investigated signals, the desired one and interferers in the baseband can be given as

(1)\begin{align} s(t) &= e^{(2\pi f_c^\mathrm{com} t + \pi \mu t^2 + \phi)}, \quad 0 \leq t \lt T_\mathrm{com} \end{align}

(2)\begin{align} i_j(t) &= e^{(2\pi f_{c_j} t + \pi \mu_j t^2 + \phi_j)}, \quad 0 \leq t \lt T_j \end{align}

Figure 5. Exemplary detection of three different chirp signals with unique slopes $\{\mu_1$, µ ₂, $\mu_3, \mu_4\}$ [1].

where $T_\mathrm{com}$ is the time duration of the communication section, µ is the chirp rate, $f_c^{\mathrm{com}}$ is the center frequency of the communication section, and ϕ is the initial phase. Besides, T_j is the time duration of the interferer, $f_{c_j}^{\mathrm{com}}$ is the center frequency of the interferer, µ_j is the chirp rate of the interferer, and ϕ_j is the initial phase. $T_\mathrm{com}$ and T_j are adjusted to have the same length in samples to be added together as

(3)\begin{align} s_\mathrm{in}(t) = s(t) + i_j(t). \end{align}

After the received signal related to $B_\mathrm{com}$ in Fig. 4 at the receiver side, only N samples of the received signal are employed to estimate the investigated chirp rates. The parameters can be evaluated regarding the following equation:

(4)\begin{align} s_\mathrm{cr}(k,\Gamma) &= \sum_{n=0}^{N-1} s_\mathrm{in}(n)~z^{(\Gamma)}~{W_N^{kn}} + w(n), \end{align}

where $s_\mathrm{in}(n)$ is the sampled signal at the output of the filter dedicated to the modulation bandwidth $B_\mathrm{com}$, $s_\mathrm{cr}(k,\Gamma)$ represents the output of the first stage of the proposed method. $z^{(\Gamma)}=e^{-\mathrm{j}\frac{2\pi\Gamma\Delta}{N}n^2}$ represents the chirp function and ${W_N^{kn}}~=~e^{-\mathrm{j}\frac{2\pi kn}{N}}$ is the Fourier factor. w(n) is the noise, $k,n = 0,..., N-1$, as introduced in DFT, and $\Gamma = 0,...,\frac{N}{\Delta}-1$, where Δ is an incremental step introduced for the estimation of the chirp rates dependent on the slopes assigned in the investigation.

Correlation-based synchronization

As a next step upon extracting the number of the signals transmitted in the same time duration, the start point of the frame is detected according to a modified version of the Schmidl & Cox algorithm [19], as proposed in [8, 20]. Since the investigation focuses on analyzing the impact of interfering signals on the desired frame synchronization, the proposed algorithm in [8] is explored based on [21], where the investigation in [21] presented the impact of narrowband interferers on the desired signals. After that, a set of different up- and down-chirps are adopted based on the parameters of a reference codebook within the sampled receiver bandwidth $B_\mathrm{com}$. In this context, the received signal is correlated with each set of up- and down-chirps deployed from the codebook. Figure 6 illustrates an exemplary output of the correlator according to the desired signal that should be synchronized at the receiver side to deliver the communication data afterward. The frequency offset $\Delta f_\mathrm{i}$ of the first set can be calculated dependent on the difference between the maximum correlation peaks of the up- and down-chirps $\Delta C_\mathrm{i}$, which are represented in samples

(5)\begin{align} \Delta f_\mathrm{i} &= \Big(\Delta C_\mathrm{i}\cdot\frac{1}{f_\mathrm{s}}-T_\mathrm{C}\Big)\cdot\mu, \end{align}

Figure 6. Exemplary time shift τ at the output of the correlator for four successive up and down-chirps, composing one preamble dedicated to synchronization correlated with the reference signals. Red peaks represent the output of the correlator concerning the up-chirps, whereas blue counterparts are the output related to down-chirps. For simplicity, only the peaks for one assigned signal are illustrated [1].

where µ is the chirp rate, $T_\mathrm{C}$ is the chirp duration, and $f_\mathrm{s}$ represents the sampling frequency. Furthermore, a modified version of the study in [20] is adopted to accomplish high accuracy in terms of frequency estimation. For accurate time estimation in each time duration, the delay $\Delta t$ in samples relative to each correlation peak can be calculated by:

(6)\begin{align} \Delta t_\mathrm{i}\cdot f_\mathrm{s} &= C_\mathrm{i} - \Big(\frac{\Delta f_\mathrm{i}}{f_\mathrm{s}}\Big). \end{align}

Measurement results

The measurements are conducted at the Institute of Radio Frequency Engineering and Electronics (IHE). A front end is employed in the frequency of ${79}\,\mathrm{GHz}$ and system-on-a-chip (SoC) platform, Zynq UltraScale + RFSoC ZCU111 from Xilinx, Inc. is adopted to emulate the transmitter, the interferers, and the receiver of the communication-assisted radar system [22]. The measurements in this paper extend their counterparts in [1], where the investigation was carried out in the baseband ${1}\,\mathrm{GHz}$. According to this, Fig. 7(a) highlights the changes in the block diagram of the adopted measurement concept since the investigation in [1] did not comprise the front end. Figure 7(b) illustrates the measurement setup in the laboratory, where the Radio Frequency System-on-Chip (RFSoC) (Field Programmable Gate Arrays [FPGA], Digital to Analog Converters [DACs], and Analog to Digital Converters [ADCs])has been controlled with MATLAB interface. Besides, two sub-harmonic mixers, a frequency multiplier, and amplifiers are used to generate the signal at the desired frequency of ${79}\,\mathrm{GHz}$. On the transmitter side, a signal generator generates the desired local oscillator (LO)signals at ${9.75}\,\mathrm{GHz}$. The signal is multiplied by a frequency multiplier included in the setup to enable the generation of signals at higher frequencies ${38}\,\mathrm{GHz}$. Since the setup adopts subharmonic mixers, the signal is generated at ${79}\,\mathrm{GHz}$ by a mixer at the transmitter chain. Besides, a power amplifier (PA) is used to amplify the transmit signal. Afterward, an E-band horn antenna is incorporated to radiate the examined signal into the medium. The transmit signal is attenuated according to the adopted frequency and received by another E-band horn antenna. An Low-noise amplifier (LNA)is employed to enhance the sensitivity of the received signal, which is downconverted with a second subharmonic mixer into the baseband domain. The same LO signal in the transmitter is adopted into receiver chains through a power divider, which splits the LO signal into two with equal power levels (${-3}\,\mathrm{dB}$). In the baseband, the RFSoC is incorporated, which consists of a high-performance FPGA, fast DACs, and ADCs. In addition, LPFs and DC blocks are incorporated into the measurement setup to filter out unwanted high-frequency components and block any DC offset, respectively. The measurements have employed various parameters adopted by current automotive radar sensors. For this purpose, the maximum analyzed bandwidth $B_\mathrm{com}$ has been assigned to ${100}\,\mathrm{MHz}$ and the maximum sampling frequency amounts to ${100}\,\mathrm{MHz}$. According to [18] regarding the level of interference, the duration of the investigated signals is uniquely varied between 10 and 100 μs with a maximum degree of interference $\kappa_\mathrm{int} = 3$ representing the number of interferers in the same time duration spanning together with the desired signal. Fig. 7(c) and (d) illustrates the results based on the proposed synchronization method [1]. As a first step, the number of interferers is detected by the FQPT algorithm according to the examined scenario in (1) and Fig. 5, where the results are compared with their counterparts in [1]. In Fig. 7(c), the correlation metric ($\mathrm{CM}$) is depicted after applying the modified version of Schmidl & Cox algorithm for frame synchronization. In this context, several cases are investigated with the same time shift dependent on the degree of the occurred interference, where $\kappa_\mathrm{int}$ represents the number of interferers contributing to the transmission with the scenario. Figure 7(c) shows that if the setup does not undergo any interference, the normalized value of ($\mathrm{CM}$) reaches its maximum. On the other hand, the value drops relative to the contributed interference. Therefore, the slopes should be uniquely employed to reduce the impact of the interference on the desired signal as far as possible. When $\kappa_\mathrm{int} = 1$, the value of ($\mathrm{CM}$) reaches approximately 0.7, where the values for both in baseband [1] and the front end at ${79}\,\mathrm{GHz}$ are nearly comparable. On the other hand, If $\{\kappa_\mathrm{int}, \kappa^\mathrm{FE}_\mathrm{int}\} = 3$, the maximum value of the normalized $\mathrm{CM}$ is less than (0.3). Furthermore, Fig. 7(d) presents various curves concerning the frequency synchronization between two communicating CaCS nodes. The level of interference in the system significantly impacts the synchronization, as indicated by the mean square error ($\mathrm{MSE}$) normalized by the sampling frequency. If $\kappa_\mathrm{int} = 1$, synchronization can be successfully achieved across the given signal-to-noise ratio (SNR)values. Conversely, with $\kappa_\mathrm{int} = 3$, appropriate SNR values are necessary to ensure frequency synchronization, reaching an $\mathrm{MSE}$ below (10⁻⁶) for $\mathrm{SNR}\leq {8}\,\mathrm{dB}$. The curves for both the baseband and ${79}\,\mathrm{GHz}$ frequencies are almost identical for both $\kappa_\mathrm{int}$ values. Besides, the deviations witnessed in the curves under $\{\kappa_\mathrm{int},~\kappa^\mathrm{FE}_\mathrm{int}\}~=~3$ interference conditions provide valuable insights into the proposed approach, where the confidence intervals (CIs) are illustrated with shaded sectors in Fig. 7(c) and (d). Both results from [1] and the current investigation show almost similar results, which prove the proposed concept. Since many simulations and measurements are carried out, a deviation based on the position of the signal of the interferer in the time-frequency plane can be pointed out along with the CI, as shown in Fig. 7(c) for $\kappa_\mathrm{int}=3$ and Fig. 7(d) for $\kappa_\mathrm{int}=1$. It should be mentioned that since the RFSoC can save a limited number of samples, the scenario comprised about 128 successive chirps, and a higher number could deliver a better result regarding the CI. In addition, if $\kappa_\mathrm{int} \gt 3$, the synchronization quality deteriorates in both time and frequency scales.

Figure 7. Measurement setup and results for time-frequency synchronization according to the proposed method. Dashed black: theoretical curve for synchronization without interference $\kappa^\mathrm{th}_\mathrm{int}=0$, blue: measured curve according for synchronization without interference $\kappa_\mathrm{int}=0$, red: synchronization with one interferer $\kappa_\mathrm{int}=1$, and green: synchronization with three interferers $\kappa_\mathrm{int}=3$. (a), (b) Measurement setup. (c) Remaining time error based on frame synchronization w.r.t correlation metric (ME). (d) Remaining frequency error based on normalized MSE.

Conclusion

This paper presents comprehensive analyses of interference impact on CaCS-based systems. A graph-based approach is adopted to compare this impact on communication and radar receivers since CaCS-based systems comprise both functionalities. In this sense, a color mapping scheme is employed with simulations in MATLAB to highlight the limited influence of interference on the communication functionality compared to its counterpart on radar. Besides, a time-frequency method for interference detection and its impact on the synchronization in CaCS systems employed with an ${79}\,\mathrm{GHz}$ measurement setup is presented. The proposed method adopts FQPT to detect the overlapping signals in the same time duration and a correlation-based approach for time-frequency synchronization. Since the bandwidth assigned for the communication is narrow, the synchronization can be accomplished with a moderate grade of coexisting interference $\kappa_\mathrm{int}\leq3$.