Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-30T19:50:21.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimised uncertainty and cost operating characteristics: newtools for conformity assessment. Application to geometrical product control in automobileindustry

Published online by Cambridge University Press:  17 December 2010

L. R. Pendrill
L. R. Pendrill*
Affiliation:
SP Technical Research Institute of Sweden, Measurement Technology, Box 857, SE-501 15 Borås, Sweden
*
⋆ Correspondence:[email protected]
Get access

Abstract

Translating measurement uncertainty into terms of effective impact associated withmanufacture, testing and incorrect assessment gives a more “stakeholder” motivated (andultimately optimised) approach to decision-making in conformance assessment. Recentlydeveloped decision-theory tools include the “optimized uncertainty” methodology and the“operating cost characteristic”. Overall costs, E, consisting of a sum oftesting costs, D, and the costs, C, associated withcustomer risk, can be calculated with the expression:

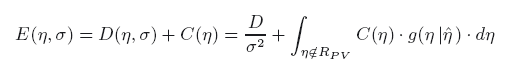
with 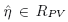, whereRPV denotes the region of permissiblevalues and σ is a measure of dispersion. A complete, 3D surface ofoverall cost can indicate the optimum level of measurement effort of these two ranges, asrecently published by the author in a wide range of applications: optimized acceptancesampling; optimized testing of measurement instruments; and an analysis of optimisedcalibration intervals and “guard-banding”. This approach is illustrated in the presentwork for the example of geometrical product control in the car industry, specifically thegap in vehicle closure panels taking account of customer dissatisfaction.

Keywords

OptimiseduncertaintycostGPSautomobile
Type
Research Article
Information
International Journal of Metrology and Quality Engineering , Volume 1 , Issue 2 , 2010 , pp. 105 - 110
Copyright
© EDP Sciences 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

Swyt, D., Metrological Issues in Precision-Tolerance Manufacturing: A Report of a NIST Industry-Needs Workshop, J. Res. NIST 98, 245–252 (1993) CrossRefGoogle Scholar
Fearn, T., Fisher, S., Thompson, M., Ellison, S., A decision-theory approach to fitness for purpose in analytical measurement, Analyst 127, 818–824 (2002) CrossRefGoogle ScholarPubMed
L.R. Pendrill, Operating “cost” characteristics in sampling by variable and attribute, Accred. Qual. Assur., http://dx.doi.org/10.1007/s00769-008-0438-y (2008)
Pendrill, L.R., Källgren, H., Optimised measurement uncertainty and decision-making in the metering of energy, fuel and exhaust gases, Izmerite’lnaya Technika (Measurement Techniques) 51, 370–377 (2008), http://dx.doi.org/10.1007/s11018-008-9047-8Google Scholar
Pendrill, L.R., Optimised measurement uncertainty and decision-making in conformity assessment, NCSLi Measure 2, 76–86 (2007) Google Scholar
Pendrill, L.R., Optimised measurement uncertainty and decision-making when sampling by variables or by attribute, Measurement 39, 829–840 (2006), Advanced Mathematical Tools for Measurement in Metrology and Testing, http://dx.doi.org/10.1016/j.measurement.2006.04.014CrossRefGoogle Scholar
L.R. Pendrill, H. Källgren, Decision-making with uncertainty in attribute sampling, Advanced Mathematical and Computational Tools in Metrology VII, in Series on Advances in Mathematics for Applied Sciences (World Scientific, Singapore, 2006), Vol. 72, pp. 212–220
Pendrill, L.R. and Källgren, H, Exhaust gas analysers and optimised sampling, uncertainties and costs, Accred. Qual. Assur. 11, 496–505 (2006), http://dx.doi.org/10.1007/s00769-006-0163-3CrossRefGoogle Scholar
http://metrology.wordpress.com/measurement-process-index/geometrical-product-specifications-gps/
ISO 14253-1:1998, Geometrical Product Specification (GPS) – Inspection by measurement of workpieces and measuring instruments – Part 1: Decision rules for proving conformance or non-conformance with specifications.
JCGM WG1, Evaluation of measurement data – The role of measurement uncertainty in deciding conformance to specified requirements, draft GUM Supplement JCGM 106 March 2010, Joint Committee for Guides in Metrology, http://www.bipm.org/en/committees/jc/jcgm/
http://www.perceptron.com/downloads/AutoFitprofile.pdf
D.C. Montgomery, Introduction to Statistical Quality Control (John Wiley & Sons, Hoboken, NJ, 1996)
G. Taguchi, Taguchi on Robust Technology (ASME Press, New York, 1993)