Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-19T02:45:16.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotational Velocity Dispersion in the Hyades and Other Galactic Clusters From The V Sin I Observations

Published online by Cambridge University Press:  12 April 2016

Yves Gaigé
Yves Gaigé*
Affiliation:
Observatoire Midi-Pyrénées

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let us recall briefly the main points of the theory as developped by Chandrasekhar and Münch (1950): if the axis of rotation of a star is inclined with an angle i to the line of sight, the apparent velocity is given by y = v sin i where v is the true rotational velocity. Assuming that the axes of rotation are randomly distributed in space, the frequency function f(v) of the true velocities may be related to the corresponding φ(y) of the apparent ones by the integral equations:

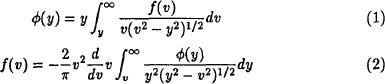
The central moments of f(v) can be derived directly from the observations by means of (1) without the knowledge of the function itself; for instance, the mean and the mean square deviation are given respectively by:

Type
IV. Input physics and basic stellar data
Information
International Astronomical Union Colloquium , Volume 137: Inside the Stars , 1993 , pp. 377 - 379
Copyright
Copyright © Astronomical Society of the Pacific 1993

References

Chandrasekhar, S., and Münch, G. 1950 Ap. J., 1ll, 142.CrossRefGoogle Scholar
Mermilliod, J.C. 1991 Private Communication Google Scholar